We consider the ordinary or fractional Laplacian plus a homogeneous, scaling-critical drift term. This operator is non-symmetric but homogeneous, and generates scales of Lp-Sobolev spaces which we compare with the ordinary homogeneous Sobolev spaces. Unlike in previous studies concerning Hardy operators, i.e. ordinary or fractional Laplacians plus scaling-critical scalar perturbations, handling the drift term requires an additional, possibly technical, restriction on the range of comparable Sobolev spaces, which is related to the unavailability of gradient bounds for the associated semigroup.
ISSN: 1361-6544
Published jointly with the London Mathematical Society, Nonlinearity covers the interdisciplinary nature of nonlinear science, featuring topics which range from physics, mathematics and engineering through to biological sciences.
Cover credit: Alexander Blokh et al 2025 38 075014
The Anh Bui et al 2026 Nonlinearity 39 015021
Marta Dell’Atti and Thomas Kecker 2026 Nonlinearity 39 015007
The geometric approach for Painlevé and quasi-Painlevé differential equations in the complex plane is applied to non-autonomous Hamiltonian systems, quartic in the dependent variables. By computing their defining manifolds (analogue of the Okamoto’s space of initial conditions in the quasi-Painlevé case), we provide a classification of such systems. We distinguish the various cases by the local behaviour at the movable singularities of the solutions, which are algebraic poles or ordinary poles. The principal cases are categorised by the initial base points of the system in the extended phase space 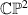 and their multiplicities, arising from the coalescence of 4 simple base points in the generic case. Through the mechanisms of coalescence of base points and degeneration (by setting certain coefficient functions in the Hamiltonian to 0), all possible sub-cases of quartic Hamiltonian systems with the quasi-Painlevé property are obtained, and are characterised by their corresponding Newton polygons. As particular sub-cases we recover certain systems equivalent to known Painlevé equations, or variants thereof. The resulting picture is a multi-faceted description of each case: the local behaviour around singularities, the surface type, and the Newton polygon.
and their multiplicities, arising from the coalescence of 4 simple base points in the generic case. Through the mechanisms of coalescence of base points and degeneration (by setting certain coefficient functions in the Hamiltonian to 0), all possible sub-cases of quartic Hamiltonian systems with the quasi-Painlevé property are obtained, and are characterised by their corresponding Newton polygons. As particular sub-cases we recover certain systems equivalent to known Painlevé equations, or variants thereof. The resulting picture is a multi-faceted description of each case: the local behaviour around singularities, the surface type, and the Newton polygon.
Alex Blumenthal and Manh Khang Huynh 2026 Nonlinearity 39 015015
In 1959, Batchelor gave a prediction for the power spectral density of a passive scalar advected by an incompressible fluid exhibiting shear-straining, a mechanism for the creation of small scales in the scalar (Batchelor 1959 J. Fluid Mech. 5 113–133). Recently, a ‘cumulative’ version of this law, summing over Fourier modes below a given wavenumber N, was given for a broad class of passive scalars under incompressible advection, including by solutions to the stochastic Navier–Stokes equations (Bedrossian et al 2022 Commun. Pure Appl. Math. 75 1237–91). This paper addresses to what extent Fourier mass of such passive scalars truly saturates the predicted power law scaling due to Batchelor. Via discrete-time pulsed-diffusion models of the advection-diffusion equations, we exhibit situations compatible with the cumulative law but for which the distribution of Fourier mass among wavenumbers 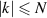 is relatively sparse, largely confined to a narrow cone in frequency space and badly violating the ‘mode-wise’ version of Batchelor’s original prediction. In the same situations we also establish an ‘exponential radial shell’ version of Batchelor’s laws via a novel application of the method of spectral distributions.
is relatively sparse, largely confined to a narrow cone in frequency space and badly violating the ‘mode-wise’ version of Batchelor’s original prediction. In the same situations we also establish an ‘exponential radial shell’ version of Batchelor’s laws via a novel application of the method of spectral distributions.
Damla Buldağ et al 2026 Nonlinearity 39 015027
We prove that if a topological dynamical system (X, T) is surjective and has the vague specification property, then its ergodic measures are dense in the space of all invariant measures. The vague specification property generalises Bowen’s classical specification property and encompasses the majority of the extensions of the specification property introduced so far. The proof proceeds by first considering the natural extension XT of (X, T) as a subsystem of the shift action on the space 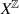 of X-valued bi-infinite sequences. We then construct a sequence of subsystems of
of X-valued bi-infinite sequences. We then construct a sequence of subsystems of 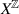 that approximate XT in the Hausdorff metric induced by a metric compatible with the product topology on
that approximate XT in the Hausdorff metric induced by a metric compatible with the product topology on 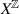 . The approximating subsystems consist of δ-chains for δ decreasing to 0. We show that chain mixing implies that each approximating system possesses the classical periodic specification property. Furthermore, we use vague specification to prove that our approximating subsystems of
. The approximating subsystems consist of δ-chains for δ decreasing to 0. We show that chain mixing implies that each approximating system possesses the classical periodic specification property. Furthermore, we use vague specification to prove that our approximating subsystems of 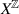 converge to XT in the Hausdorff metric induced by the Besicovitch pseudometric. It follows that the simplices of invariant measures of these subsystems of δ-chains converge to the simplex of invariant measures of XT with respect to a generalised version of Ornstein’s
converge to XT in the Hausdorff metric induced by the Besicovitch pseudometric. It follows that the simplices of invariant measures of these subsystems of δ-chains converge to the simplex of invariant measures of XT with respect to a generalised version of Ornstein’s 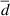 metric. What is more, the density of ergodic measures is preserved in the limit. The proof concludes by observing that the simplices of invariant measures for XT and (X, T) coincide. The approximation technique developed in this paper appears to be of independent interest.
metric. What is more, the density of ergodic measures is preserved in the limit. The proof concludes by observing that the simplices of invariant measures for XT and (X, T) coincide. The approximation technique developed in this paper appears to be of independent interest.
Antoine Barlet et al 2026 Nonlinearity 39 015018
Chaotic systems are characterised by exponential separation between close-by trajectories, which in particular leads to deterministic unpredictability over an infinite time-window. It is now believed, that such butterfly effect is not fully relevant to account for the type of randomness observed in turbulence. For example, tracers in homogeneous isotropic flows are observed to separate algebraically, following an universal growth, independent from the initial separation. This regime, known as Richardon’s regime, suggests that at the level of trajectories, and unlike in chaos theory, randomness may in fact emerge in finite-time. This phenomenon called ‘spontaneous stochasticity’ originates from the singular nature of the underlying dynamics, and provides a candidate framework for turbulent randomness and transport. While spontaneous stochasticity has been mathematically formalised in simplified turbulence models, a precise and systematic tool for quantifying the various facets of this phenomenon is to this day missing. In particular, it is still unclear whether chaos is important for that behaviour to appear. In this paper we introduce a 3d rough flow that can be tuned to present Lagrangian chaos. The flow is inspired by the Weierstrass function and is entitled ‘the WABC model’. After analysing its properties, we define what is spontaneous stochasticity in this context. The provided formal definition is then adapted to better suit for numerical analysis. We present the results from Monte–Carlo simulations of Lagrangian particles in this flow. Within the numerical precision, we quantitatively observe the appearance of spontaneous stochasticity in this model. We investigate the influence of noise type and find that the observed spontaneous stochasticity does not depend on the chosen stochastic regularisations.
Gavin Stewart 2026 Nonlinearity 39 015025
We consider solutions to the Benjamin–Ono equation 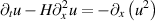 that are localized in a reference frame moving to the right with constant speed. We show that any such solution that decays at least like
that are localized in a reference frame moving to the right with constant speed. We show that any such solution that decays at least like 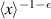 for some ε > 0 in a comoving coordinate frame must in fact decay like
for some ε > 0 in a comoving coordinate frame must in fact decay like 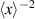 . In view of the explicit soliton solutions, this decay rate is sharp. Our proof has two main ingredients. The first is microlocal dispersive estimates for the Benjamin–Ono equation in a moving frame, which allow us to prove spatial decay of the solution provided the nonlinearity has sufficient decay. The second is a careful normal form analysis, which allows us to obtain rapid decay of the nonlinearity for a transformed equation assuming only modest decay of the solution. Our arguments are entirely time dependent, and do not require the solution to be an exact travelling wave.
. In view of the explicit soliton solutions, this decay rate is sharp. Our proof has two main ingredients. The first is microlocal dispersive estimates for the Benjamin–Ono equation in a moving frame, which allow us to prove spatial decay of the solution provided the nonlinearity has sufficient decay. The second is a careful normal form analysis, which allows us to obtain rapid decay of the nonlinearity for a transformed equation assuming only modest decay of the solution. Our arguments are entirely time dependent, and do not require the solution to be an exact travelling wave.
Matheus M Castro and Giuseppe Tenaglia 2026 Nonlinearity 39 015026
In this paper, we study the random dynamical system 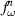 generated by a family of maps
generated by a family of maps ![$\{f_{\omega_0}: \mathbb{S}^1 \to \mathbb{S}^1\}_{\omega_0 \in [-\varepsilon,\varepsilon]},$](https://content.cld.iop.org/journals/0951-7715/39/1/015026/revision1/nonae3418ieqn2.gif)
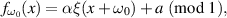 where
where 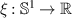 is a non-degenerate map,
is a non-degenerate map, 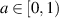 , and
, and 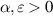 . Fixing a constant
. Fixing a constant 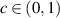 , we show that for α sufficiently large and for
, we show that for α sufficiently large and for 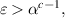 the random dynamical system
the random dynamical system 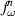 admits a random Young tower structure and exhibits quenched exponential decay of correlations.
admits a random Young tower structure and exhibits quenched exponential decay of correlations.
Romain Aimino et al 2026 Nonlinearity 39 015023
We establish a theory for multivariate extreme value analysis of dynamical systems. Namely, we provide conditions adapted to the dynamical setting which enable the study of dependence between extreme values of the components of 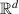 -valued observables evaluated along the orbits of the systems. We study this cross-sectional dependence, which results from the combination of a spatial and a temporal dependence structures. We give several illustrative applications, where concrete systems and dependence sources are introduced and analysed.
-valued observables evaluated along the orbits of the systems. We study this cross-sectional dependence, which results from the combination of a spatial and a temporal dependence structures. We give several illustrative applications, where concrete systems and dependence sources are introduced and analysed.
Luigi De Rosa et al 2026 Nonlinearity 39 025002
We consider weak solutions to the incompressible Euler equations. It is shown that energy conservation holds in any Onsager critical class in which smooth functions are dense. The argument is independent of the specific critical regularity and the underlying PDE. This groups several energy conservation results and it suggests that critical spaces where smooth functions are dense are not at all different from subcritical ones, although possessing the ‘minimal’ regularity index. Then, we study properties of the dissipation D in the case of bounded solutions that are allowed to jump on 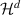 -rectifiable space-time sets Σ, which are the natural dissipative regions in the compressible setting. As soon as both the velocity and the pressure possess traces on Σ, it is shown that Σ is D-negligible. The argument makes the role of the incompressibility very apparent, and it prevents dissipation on codimension 1 sets even if they happen to be densely distributed. As a corollary, we deduce energy conservation for bounded solutions of ‘special bounded deformation’, providing the first energy conservation criterion in a critical class where only an assumption on the ‘longitudinal’ increment is made, while the energy flux does not vanish for kinematic reasons.
-rectifiable space-time sets Σ, which are the natural dissipative regions in the compressible setting. As soon as both the velocity and the pressure possess traces on Σ, it is shown that Σ is D-negligible. The argument makes the role of the incompressibility very apparent, and it prevents dissipation on codimension 1 sets even if they happen to be densely distributed. As a corollary, we deduce energy conservation for bounded solutions of ‘special bounded deformation’, providing the first energy conservation criterion in a critical class where only an assumption on the ‘longitudinal’ increment is made, while the energy flux does not vanish for kinematic reasons.
Reza Mohammadpour and Anthony Quas 2026 Nonlinearity 39 015014
We consider the one-step matrix cocycle generated by a particular pair of non-negative parabolic matrices and study the equilibrium measures for 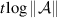 as t runs over the reals. We show that there is a freezing first order phase transition at
as t runs over the reals. We show that there is a freezing first order phase transition at 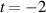 so that for
so that for 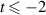 the equilibrium measure is non-unique and supported on the two fixed points, while for
the equilibrium measure is non-unique and supported on the two fixed points, while for 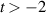 , the equilibrium measure is unique, non-atomic and fully supported. The phase transition closely resembles the classical Hofbauer example. In particular, our example shows that there may be non-unique equilibrium measures for negative t even if the cocycle is strongly irreducible and proximal.
, the equilibrium measure is unique, non-atomic and fully supported. The phase transition closely resembles the classical Hofbauer example. In particular, our example shows that there may be non-unique equilibrium measures for negative t even if the cocycle is strongly irreducible and proximal.
Sergio Moroni 2026 Nonlinearity 39 025007
We present a stability result for groundstates of a Schrödinger–Poisson system in 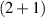 dimension, modelling the propagation of a light beam through a liquid crystal with nonlocal nonlinear response. The core of the proof is a coercivity bound on the second derivative of the action, where non scaling nonlinearities and the coupled system present the major difficulties. In addition we prove existence of a ground state with frequency σ for any
dimension, modelling the propagation of a light beam through a liquid crystal with nonlocal nonlinear response. The core of the proof is a coercivity bound on the second derivative of the action, where non scaling nonlinearities and the coupled system present the major difficulties. In addition we prove existence of a ground state with frequency σ for any 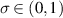 as a minimal point over an appropriate Nehari manifold.
as a minimal point over an appropriate Nehari manifold.
Tsukasa Iwabuchi and Taiki Okazaki 2026 Nonlinearity 39 025006
We consider the uniqueness of the solution of the dissipative surface quasi-geostrophic equation. We show that the uniqueness holds in non-homogeneous Besov spaces without any additional assumption which is supposed to construct solutions. When the power of the fractional Laplacian is close to 2, we prove that the uniqueness with the regularity index 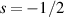 . We extract the least regularity
. We extract the least regularity 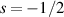 for the well-definedness of the nonlinear term of the equation.
for the well-definedness of the nonlinear term of the equation.
Pierre Guiraud et al 2026 Nonlinearity 39 025005
We consider a family of piecewise contractions admitting a rotation number and defined for every 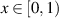 by
by 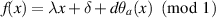 , where
, where 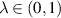 ,
, 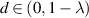 ,
, ![$\delta\in[0,1]$](https://content.cld.iop.org/journals/0951-7715/39/2/025005/revision1/nonae3b8dieqn5.gif) ,
, ![$a\in[0,1]$](https://content.cld.iop.org/journals/0951-7715/39/2/025005/revision1/nonae3b8dieqn6.gif) and
and 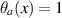 if
if 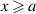 and
and 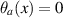 otherwise. In the special case where a = 1, the family reduces to the well studied ‘contracted rotations’
otherwise. In the special case where a = 1, the family reduces to the well studied ‘contracted rotations’ 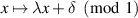 , which are 2-interval piecewise λ-affine contractions when
, which are 2-interval piecewise λ-affine contractions when 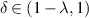 . Considering
. Considering 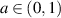 allows maps with an additional discontinuity, that is, 3-interval piecewise λ-affine contractions. Supposing λ and d fixed, for any
allows maps with an additional discontinuity, that is, 3-interval piecewise λ-affine contractions. Supposing λ and d fixed, for any 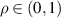 and
and ![$\alpha\in[0,1]$](https://content.cld.iop.org/journals/0951-7715/39/2/025005/revision1/nonae3b8dieqn14.gif) , we provide the values of the parameters δ and a for which the corresponding map has rotation number ρ, and a symbolic dynamics containing that of the rotation
, we provide the values of the parameters δ and a for which the corresponding map has rotation number ρ, and a symbolic dynamics containing that of the rotation 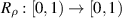 of angle ρ with respect to the partition given by the positions of
of angle ρ with respect to the partition given by the positions of 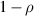 and α in
and α in 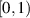 . This enables in particular to determine the maps that have a given number of periodic orbits of an arbitrary period, or a Cantor set attractor supporting a dynamics of a given complexity.
. This enables in particular to determine the maps that have a given number of periodic orbits of an arbitrary period, or a Cantor set attractor supporting a dynamics of a given complexity.
Fashun Gao et al 2026 Nonlinearity 39 025004
In this paper, we study the existence of nontrivial solutions of the following coupled Hartree system 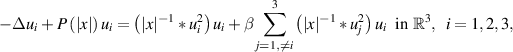 where P(r) is the positive radial potential and
where P(r) is the positive radial potential and 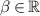 is a coupling parameter. We prove the existence of non-radial segregated solutions for the coupled Hartree system with weak interspecies forces under suitable conditions on the linear potential P(r) by applying Lyapunov–Schmidt reduction method.
is a coupling parameter. We prove the existence of non-radial segregated solutions for the coupled Hartree system with weak interspecies forces under suitable conditions on the linear potential P(r) by applying Lyapunov–Schmidt reduction method.
Lu Chen et al 2026 Nonlinearity 39 025003
In this paper, we consider the following Hardy-type mean field equation
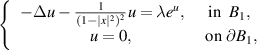 where λ > 0 is small and B1 is the standard unit disc of
where λ > 0 is small and B1 is the standard unit disc of 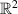 . Applying the moving plane method of hyperbolic space and the accurate expansion of heat kernel on hyperbolic space, we establish the radial symmetry and Brezis–Merle lemma for solutions of Hardy-type mean field equation. Meanwhile, we also derive the quantitative results for solutions of Hardy-type mean field equation, which improves significantly the compactness results for classical mean field equation obtained by Brezis–Merle and Li–Shafrir. Furthermore, applying the local Pohozaev identity from scaling, blow-up analysis and a contradiction argument, we prove that the solutions are unique when λ is sufficiently close to 0.
. Applying the moving plane method of hyperbolic space and the accurate expansion of heat kernel on hyperbolic space, we establish the radial symmetry and Brezis–Merle lemma for solutions of Hardy-type mean field equation. Meanwhile, we also derive the quantitative results for solutions of Hardy-type mean field equation, which improves significantly the compactness results for classical mean field equation obtained by Brezis–Merle and Li–Shafrir. Furthermore, applying the local Pohozaev identity from scaling, blow-up analysis and a contradiction argument, we prove that the solutions are unique when λ is sufficiently close to 0.
Daniel Smania 2025 Nonlinearity 38 082001
Deterministic dynamical systems often exhibit behaviours that appear random and unpredictable, blending order and chaos in intricate ways. Traditional methods for analysing these systems struggle with systems featuring irregularities like discontinuities, singularities, or difficult-to-analyze invariant measures. This survey explores the application of transfer operator methods, Besov spaces and measure spaces with grids as tools for addressing these challenges. Focusing on piecewise expanding maps as a key example, we demonstrate how these methods provide a flexible framework for studying statistical properties of dynamical systems in irregular settings. Besov spaces capture localised irregularities, while measure spaces with grids facilitate systematic discretisation and computational analysis. Together, these tools offer a powerful approach to understanding the intricate interplay between deterministic dynamics and statistical regularities.
Ryan Goh and Arnd Scheel 2023 Nonlinearity 36 R1
Pattern forming systems allow for a wealth of states, where wavelengths and orientation of patterns varies and defects disrupt patches of monocrystalline regions. Growth of patterns has long been recognized as a strong selection mechanism. We present here recent and new results on the selection of patterns in situations where the pattern-forming region expands in time. The wealth of phenomena is roughly organised in bifurcation diagrams that depict wavenumbers of selected crystalline states as functions of growth rates. We show how a broad set of mathematical and numerical tools can help shed light into the complexity of this selection process.
Ali Tahzibi 2021 Nonlinearity 34 R75
In this survey we recall basic notions of disintegration of measures and entropy along unstable laminations. We review some roles of unstable entropy in smooth ergodic theory including the so-called invariance principle, Margulis construction of measures of maximal entropy, physical measures and rigidity. We also give some new examples and pose some open problems.
Thomas Bothner 2021 Nonlinearity 34 R1
This article is firstly a historic review of the theory of Riemann–Hilbert problems with particular emphasis placed on their original appearance in the context of Hilbert’s 21st problem and Plemelj’s work associated with it. The secondary purpose of this note is to invite a new generation of mathematicians to the fascinating world of Riemann–Hilbert techniques and their modern appearances in nonlinear mathematical physics. We set out to achieve this goal with six examples, including a new proof of the integro-differential Painlevé-II formula of Amir et al (2011 Commun. Pure Appl. Math.64 466–537) that enters in the description of the Kardar–Parisi–Zhang crossover distribution. Parts of this text are based on the author’s Szegő prize lecture at the 15th International Symposium on Orthogonal Polynomials, Special Functions and Applications (OPSFA) in Hagenberg, Austria.
Valerio Lucarini and Tamás Bódai 2020 Nonlinearity 33 R59
For a wide range of values of the intensity of the incoming solar radiation, the Earth features at least two attracting states, which correspond to competing climates. The warm climate is analogous to the present one; the snowball climate features global glaciation and conditions that can hardly support life forms. Paleoclimatic evidences suggest that in the past our planet flipped between these two states. The main physical mechanism responsible for such an instability is the ice-albedo feedback. In a previous work, we defined the Melancholia states that sit between the two climates. Such states are embedded in the boundaries between the two basins of attraction and feature extensive glaciation down to relatively low latitudes. Here, we explore the global stability properties of the system by introducing random perturbations as modulations to the intensity of the incoming solar radiation. We observe noise-induced transitions between the competing basins of attraction. In the weak-noise limit, large deviation laws define the invariant measure, the statistics of escape times, and typical escape paths called instantons. By constructing the instantons empirically, we show that the Melancholia states are the gateways for the noise-induced transitions. In the region of multistability, in the zero-noise limit, the measure is supported only on one of the competing attractors. For low (high) values of the solar irradiance, the limit measure is the snowball (warm) climate. The changeover between the two regimes corresponds to a first-order phase transition in the system. The framework we propose seems of general relevance for the study of complex multistable systems. Finally, we put forward a new method for constructing Melancholia states from direct numerical simulations, which provides a possible alternative with respect to the edge-tracking algorithm.
Luigi De Rosa et al 2026 Nonlinearity 39 025002
We consider weak solutions to the incompressible Euler equations. It is shown that energy conservation holds in any Onsager critical class in which smooth functions are dense. The argument is independent of the specific critical regularity and the underlying PDE. This groups several energy conservation results and it suggests that critical spaces where smooth functions are dense are not at all different from subcritical ones, although possessing the ‘minimal’ regularity index. Then, we study properties of the dissipation D in the case of bounded solutions that are allowed to jump on 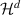 -rectifiable space-time sets Σ, which are the natural dissipative regions in the compressible setting. As soon as both the velocity and the pressure possess traces on Σ, it is shown that Σ is D-negligible. The argument makes the role of the incompressibility very apparent, and it prevents dissipation on codimension 1 sets even if they happen to be densely distributed. As a corollary, we deduce energy conservation for bounded solutions of ‘special bounded deformation’, providing the first energy conservation criterion in a critical class where only an assumption on the ‘longitudinal’ increment is made, while the energy flux does not vanish for kinematic reasons.
-rectifiable space-time sets Σ, which are the natural dissipative regions in the compressible setting. As soon as both the velocity and the pressure possess traces on Σ, it is shown that Σ is D-negligible. The argument makes the role of the incompressibility very apparent, and it prevents dissipation on codimension 1 sets even if they happen to be densely distributed. As a corollary, we deduce energy conservation for bounded solutions of ‘special bounded deformation’, providing the first energy conservation criterion in a critical class where only an assumption on the ‘longitudinal’ increment is made, while the energy flux does not vanish for kinematic reasons.
Niclas Bernhoff et al 2026 Nonlinearity 39 015032
This study investigates the steady Boltzmann equation in one spatial variable for a polyatomic single-component gas in a half-space. Inflow boundary conditions are assumed at the half-space boundary, where particles entering the half-space are distributed as a Maxwellian, an equilibrium distribution characterised by macroscopic parameters of the boundary. At the far end, the gas tends to an equilibrium distribution, which is also Maxwellian. Using conservation laws and an entropy inequality, we derive relations between the macroscopic parameters of the boundary and at infinity required for the existence of solutions. The relations vary depending on the sign of the Mach number at infinity, which dictates whether evaporation or condensation takes place at the interface between the gas and the condensed phase. We explore the obtained relations numerically. This investigation reveals that, although the relations are qualitatively similar for various internal degrees of freedom of the gas, clear quantitative differences exist.
Mike R Jeffrey and Pedro C C R Pereira 2026 Nonlinearity 39 015031
Elementary catastrophes occur in scalar or gradient systems, but the same catastrophes also underlie the more intricate bifurcations of vector fields, providing a more practical means to locate and identify them than standard bifurcation theory. Here we formalise the concept of these underlying catastrophes, proving that it identifies contact-equivalent families, and we extend the concept to difference equations (i.e. maps/diffeomorphisms). We deal only with bifurcations of corank one, and centre dimension one (meaning the system has one eigenvalue equal to zero in the case of a vector field, or equal to one in the case of a map). In this case we prove moreover that these underlying catastrophes identify topological bifurcation classes. It is hoped these results point the way to extending the concept of underlying catastrophes to higher coranks and centre dimensions. We illustrate with some simple examples, including a system of biological reaction diffusion equations whose homogenous steady states are shown to undergo butterfly and star catastrophes.
Damla Buldağ et al 2026 Nonlinearity 39 015027
We prove that if a topological dynamical system (X, T) is surjective and has the vague specification property, then its ergodic measures are dense in the space of all invariant measures. The vague specification property generalises Bowen’s classical specification property and encompasses the majority of the extensions of the specification property introduced so far. The proof proceeds by first considering the natural extension XT of (X, T) as a subsystem of the shift action on the space 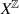 of X-valued bi-infinite sequences. We then construct a sequence of subsystems of
of X-valued bi-infinite sequences. We then construct a sequence of subsystems of 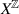 that approximate XT in the Hausdorff metric induced by a metric compatible with the product topology on
that approximate XT in the Hausdorff metric induced by a metric compatible with the product topology on 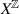 . The approximating subsystems consist of δ-chains for δ decreasing to 0. We show that chain mixing implies that each approximating system possesses the classical periodic specification property. Furthermore, we use vague specification to prove that our approximating subsystems of
. The approximating subsystems consist of δ-chains for δ decreasing to 0. We show that chain mixing implies that each approximating system possesses the classical periodic specification property. Furthermore, we use vague specification to prove that our approximating subsystems of 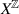 converge to XT in the Hausdorff metric induced by the Besicovitch pseudometric. It follows that the simplices of invariant measures of these subsystems of δ-chains converge to the simplex of invariant measures of XT with respect to a generalised version of Ornstein’s
converge to XT in the Hausdorff metric induced by the Besicovitch pseudometric. It follows that the simplices of invariant measures of these subsystems of δ-chains converge to the simplex of invariant measures of XT with respect to a generalised version of Ornstein’s 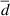 metric. What is more, the density of ergodic measures is preserved in the limit. The proof concludes by observing that the simplices of invariant measures for XT and (X, T) coincide. The approximation technique developed in this paper appears to be of independent interest.
metric. What is more, the density of ergodic measures is preserved in the limit. The proof concludes by observing that the simplices of invariant measures for XT and (X, T) coincide. The approximation technique developed in this paper appears to be of independent interest.
Matheus M Castro and Giuseppe Tenaglia 2026 Nonlinearity 39 015026
In this paper, we study the random dynamical system 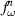 generated by a family of maps
generated by a family of maps ![$\{f_{\omega_0}: \mathbb{S}^1 \to \mathbb{S}^1\}_{\omega_0 \in [-\varepsilon,\varepsilon]},$](https://content.cld.iop.org/journals/0951-7715/39/1/015026/revision1/nonae3418ieqn2.gif)
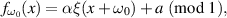 where
where 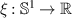 is a non-degenerate map,
is a non-degenerate map, 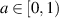 , and
, and 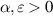 . Fixing a constant
. Fixing a constant 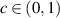 , we show that for α sufficiently large and for
, we show that for α sufficiently large and for 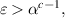 the random dynamical system
the random dynamical system 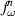 admits a random Young tower structure and exhibits quenched exponential decay of correlations.
admits a random Young tower structure and exhibits quenched exponential decay of correlations.
Gavin Stewart 2026 Nonlinearity 39 015025
We consider solutions to the Benjamin–Ono equation 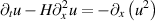 that are localized in a reference frame moving to the right with constant speed. We show that any such solution that decays at least like
that are localized in a reference frame moving to the right with constant speed. We show that any such solution that decays at least like 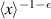 for some ε > 0 in a comoving coordinate frame must in fact decay like
for some ε > 0 in a comoving coordinate frame must in fact decay like 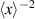 . In view of the explicit soliton solutions, this decay rate is sharp. Our proof has two main ingredients. The first is microlocal dispersive estimates for the Benjamin–Ono equation in a moving frame, which allow us to prove spatial decay of the solution provided the nonlinearity has sufficient decay. The second is a careful normal form analysis, which allows us to obtain rapid decay of the nonlinearity for a transformed equation assuming only modest decay of the solution. Our arguments are entirely time dependent, and do not require the solution to be an exact travelling wave.
. In view of the explicit soliton solutions, this decay rate is sharp. Our proof has two main ingredients. The first is microlocal dispersive estimates for the Benjamin–Ono equation in a moving frame, which allow us to prove spatial decay of the solution provided the nonlinearity has sufficient decay. The second is a careful normal form analysis, which allows us to obtain rapid decay of the nonlinearity for a transformed equation assuming only modest decay of the solution. Our arguments are entirely time dependent, and do not require the solution to be an exact travelling wave.
Romain Aimino et al 2026 Nonlinearity 39 015023
We establish a theory for multivariate extreme value analysis of dynamical systems. Namely, we provide conditions adapted to the dynamical setting which enable the study of dependence between extreme values of the components of 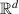 -valued observables evaluated along the orbits of the systems. We study this cross-sectional dependence, which results from the combination of a spatial and a temporal dependence structures. We give several illustrative applications, where concrete systems and dependence sources are introduced and analysed.
-valued observables evaluated along the orbits of the systems. We study this cross-sectional dependence, which results from the combination of a spatial and a temporal dependence structures. We give several illustrative applications, where concrete systems and dependence sources are introduced and analysed.
The Anh Bui et al 2026 Nonlinearity 39 015021
We consider the ordinary or fractional Laplacian plus a homogeneous, scaling-critical drift term. This operator is non-symmetric but homogeneous, and generates scales of Lp-Sobolev spaces which we compare with the ordinary homogeneous Sobolev spaces. Unlike in previous studies concerning Hardy operators, i.e. ordinary or fractional Laplacians plus scaling-critical scalar perturbations, handling the drift term requires an additional, possibly technical, restriction on the range of comparable Sobolev spaces, which is related to the unavailability of gradient bounds for the associated semigroup.
Antoine Barlet et al 2026 Nonlinearity 39 015018
Chaotic systems are characterised by exponential separation between close-by trajectories, which in particular leads to deterministic unpredictability over an infinite time-window. It is now believed, that such butterfly effect is not fully relevant to account for the type of randomness observed in turbulence. For example, tracers in homogeneous isotropic flows are observed to separate algebraically, following an universal growth, independent from the initial separation. This regime, known as Richardon’s regime, suggests that at the level of trajectories, and unlike in chaos theory, randomness may in fact emerge in finite-time. This phenomenon called ‘spontaneous stochasticity’ originates from the singular nature of the underlying dynamics, and provides a candidate framework for turbulent randomness and transport. While spontaneous stochasticity has been mathematically formalised in simplified turbulence models, a precise and systematic tool for quantifying the various facets of this phenomenon is to this day missing. In particular, it is still unclear whether chaos is important for that behaviour to appear. In this paper we introduce a 3d rough flow that can be tuned to present Lagrangian chaos. The flow is inspired by the Weierstrass function and is entitled ‘the WABC model’. After analysing its properties, we define what is spontaneous stochasticity in this context. The provided formal definition is then adapted to better suit for numerical analysis. We present the results from Monte–Carlo simulations of Lagrangian particles in this flow. Within the numerical precision, we quantitatively observe the appearance of spontaneous stochasticity in this model. We investigate the influence of noise type and find that the observed spontaneous stochasticity does not depend on the chosen stochastic regularisations.
Alex Blumenthal and Manh Khang Huynh 2026 Nonlinearity 39 015015
In 1959, Batchelor gave a prediction for the power spectral density of a passive scalar advected by an incompressible fluid exhibiting shear-straining, a mechanism for the creation of small scales in the scalar (Batchelor 1959 J. Fluid Mech.5 113–133). Recently, a ‘cumulative’ version of this law, summing over Fourier modes below a given wavenumber N, was given for a broad class of passive scalars under incompressible advection, including by solutions to the stochastic Navier–Stokes equations (Bedrossian et al 2022 Commun. Pure Appl. Math.75 1237–91). This paper addresses to what extent Fourier mass of such passive scalars truly saturates the predicted power law scaling due to Batchelor. Via discrete-time pulsed-diffusion models of the advection-diffusion equations, we exhibit situations compatible with the cumulative law but for which the distribution of Fourier mass among wavenumbers 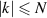 is relatively sparse, largely confined to a narrow cone in frequency space and badly violating the ‘mode-wise’ version of Batchelor’s original prediction. In the same situations we also establish an ‘exponential radial shell’ version of Batchelor’s laws via a novel application of the method of spectral distributions.
is relatively sparse, largely confined to a narrow cone in frequency space and badly violating the ‘mode-wise’ version of Batchelor’s original prediction. In the same situations we also establish an ‘exponential radial shell’ version of Batchelor’s laws via a novel application of the method of spectral distributions.
Mark J Ablowitz and Ziad H Musslimani 2016 Nonlinearity 29 915
A nonlocal nonlinear Schrödinger (NLS) equation was recently introduced and shown to be an integrable infinite dimensional Hamiltonian evolution equation. In this paper a detailed study of the inverse scattering transform of this nonlocal NLS equation is carried out. The direct and inverse scattering problems are analyzed. Key symmetries of the eigenfunctions and scattering data and conserved quantities are obtained. The inverse scattering theory is developed by using a novel left–right Riemann–Hilbert problem. The Cauchy problem for the nonlocal NLS equation is formulated and methods to find pure soliton solutions are presented; this leads to explicit time-periodic one and two soliton solutions. A detailed comparison with the classical NLS equation is given and brief remarks about nonlocal versions of the modified Korteweg–de Vries and sine-Gordon equations are made.
Rui Peng and Xiao-Qiang Zhao 2012 Nonlinearity 25 1451
In this paper, we consider a susceptible–infected–susceptible (SIS) reaction–diffusion model, where the rates of disease transmission and recovery are assumed to be spatially heterogeneous and temporally periodic and the total population number is constant. We introduce a basic reproduction number
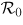 and establish threshold-type results on the global dynamics in terms of
and establish threshold-type results on the global dynamics in terms of
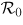 . In particular, we obtain the asymptotic properties of
. In particular, we obtain the asymptotic properties of
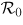 with respect to the diffusion rate dI of the infected individuals, which exhibit the delicate influence of the time-periodic heterogeneous environment on the extinction and persistence of the infectious disease. Our analytical results suggest that the combination of spatial heterogeneity and temporal periodicity tends to enhance the persistence of the disease.
with respect to the diffusion rate dI of the infected individuals, which exhibit the delicate influence of the time-periodic heterogeneous environment on the extinction and persistence of the infectious disease. Our analytical results suggest that the combination of spatial heterogeneity and temporal periodicity tends to enhance the persistence of the disease.
Anouar Bahrouni et al 2019 Nonlinearity 32 2481
In this paper we are concerned with a class of double phase energy functionals arising in the theory of transonic flows. Their main feature is that the associated Euler equation is driven by the Baouendi–Grushin operator with variable coefficient. This partial differential equation is of mixed type and possesses both elliptic and hyperbolic regions. After establishing a weighted inequality for the Baouendi–Grushin operator and a related compactness property, we establish the existence of stationary waves under arbitrary perturbations of the reaction.
Henri Berestycki et al 2009 Nonlinearity 22 2813
We consider the Fisher–KPP equation with a non-local saturation effect defined through an interaction kernel ϕ(x) and investigate the possible differences with the standard Fisher–KPP equation. Our first concern is the existence of steady states. We prove that if the Fourier transform
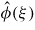 is positive or if the length σ of the non-local interaction is short enough, then the only steady states are u ≡ 0 and u ≡ 1. Next, we study existence of the travelling waves. We prove that this equation admits travelling wave solutions that connect u = 0 to an unknown positive steady state u∞(x), for all speeds c ⩾ c*. The travelling wave connects to the standard state u∞(x) ≡ 1 under the aforementioned conditions:
is positive or if the length σ of the non-local interaction is short enough, then the only steady states are u ≡ 0 and u ≡ 1. Next, we study existence of the travelling waves. We prove that this equation admits travelling wave solutions that connect u = 0 to an unknown positive steady state u∞(x), for all speeds c ⩾ c*. The travelling wave connects to the standard state u∞(x) ≡ 1 under the aforementioned conditions:
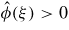 or σ is sufficiently small. However, the wave is not monotonic for σ large.
or σ is sufficiently small. However, the wave is not monotonic for σ large.
Tianxiang Gou and Louis Jeanjean 2018 Nonlinearity 31 2319
We consider the existence of multiple positive solutions to the nonlinear Schrödinger systems set on 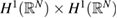 ,
,
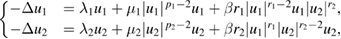
under the constraint
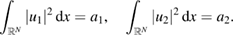
Here 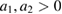 are prescribed,
are prescribed, 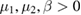 , and the frequencies
, and the frequencies 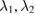 are unknown and will appear as Lagrange multipliers. Two cases are studied, the first when
are unknown and will appear as Lagrange multipliers. Two cases are studied, the first when 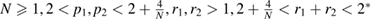 , the second when
, the second when 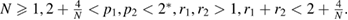 In both cases, assuming that
In both cases, assuming that 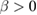 is sufficiently small, we prove the existence of two positive solutions. The first one is a local minimizer for which we establish the compactness of the minimizing sequences and also discuss the orbital stability of the associated standing waves. The second solution is obtained through a constrained mountain pass and a constrained linking respectively.
is sufficiently small, we prove the existence of two positive solutions. The first one is a local minimizer for which we establish the compactness of the minimizing sequences and also discuss the orbital stability of the associated standing waves. The second solution is obtained through a constrained mountain pass and a constrained linking respectively.
Louis Jeanjean and Sheng-Sen Lu 2019 Nonlinearity 32 4942
We study the following nonlinear scalar field equation
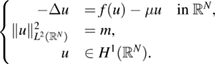
Here 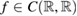 , m > 0 is a given constant and
, m > 0 is a given constant and 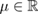 arises as a Lagrange multiplier. In a mass subcritical case but under general assumptions on the nonlinearity f , we show the existence of one nonradial solution for any
arises as a Lagrange multiplier. In a mass subcritical case but under general assumptions on the nonlinearity f , we show the existence of one nonradial solution for any 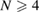 , and obtain multiple (sometimes infinitely many) nonradial solutions when N = 4 or
, and obtain multiple (sometimes infinitely many) nonradial solutions when N = 4 or 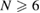 . In particular, all these solutions are sign-changing.
. In particular, all these solutions are sign-changing.
A S Fokas 2016 Nonlinearity 29 319
Two new integrable nonlocal Davey–Stewartson equations are introduced. These equations provide two-spatial dimensional analogues of the integrable, nonlocal nonlinear Schrö-dinger equation introduced in Ablowitz and Musslimani (2013 Phys. Rev. Lett. 110 064105). Furthermore, like the latter equation, they also possess a PT symmetry and, as it is well known, this symmetry is important for the occurence of such equations in nonlinear optics. A method for solving the initial value problem of these integrable equations is discussed. It is shown that the technique used for constructing these novel integrable equations has general validity; as an illustrative example, an additional two-dimensional integrable generalization of the nonlocal nonlinear Schrödinger is also presented.
Junping Shi et al 2019 Nonlinearity 32 3188
A single species spatial population model that incorporates Fickian diffusion, memory-based diffusion, and reaction with maturation delay is formulated. The stability of a positive equilibrium and the crossing curves in the two-delay parameter plane on which the characteristic equation has purely imaginary roots are studied. With Neumann boundary condition, the crossing curve that separates the stable and unstable regions of the equilibrium may consist of two components, where spatially homogeneous and inhomogeneous periodic solutions are generated through Hopf bifurcation respectively. This phenomenon rarely emerges from standard partial functional differential equations with Neumann boundary condition, which indicates that the memory-based diffusion can induce more complicated spatiotemporal dynamics.
Zexin Zhang and Zhitao Zhang 2022 Nonlinearity 35 5621
In this paper, we study the p-Laplacian equation with a Lp-norm constraint: 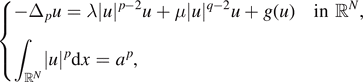 where N ⩾ 2, a > 0,
where N ⩾ 2, a > 0, 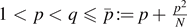 ,
, 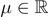 ,
, 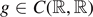 and
and 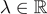 is a Lagrange multiplier, which appears due to the mass constraint ‖u‖p = a. We assume that g is odd and Lp-supercritical. When
is a Lagrange multiplier, which appears due to the mass constraint ‖u‖p = a. We assume that g is odd and Lp-supercritical. When 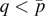 and μ > 0, we use Schwarz rearrangement and Ekeland variational principle to prove the existence of positive radial ground states for suitable μ. When
and μ > 0, we use Schwarz rearrangement and Ekeland variational principle to prove the existence of positive radial ground states for suitable μ. When 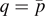 and μ > 0 or
and μ > 0 or 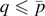 and μ ⩽ 0, with an additional condition of g, we obtain a positive radial ground state if μ lies in a suitable range, by the Schwarz rearrangement and minimax theorems. Via a fountain theorem type argument, with suitable
and μ ⩽ 0, with an additional condition of g, we obtain a positive radial ground state if μ lies in a suitable range, by the Schwarz rearrangement and minimax theorems. Via a fountain theorem type argument, with suitable 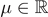 , we obtain infinitely many radial solutions for any N ⩾ 2 and establish the existence of infinitely many nonradial sign-changing solutions for N = 4 or N ⩾ 6. In any case mentioned above, the range of μ depends on the value of a: |μ| can be large if a > 0 is small.
, we obtain infinitely many radial solutions for any N ⩾ 2 and establish the existence of infinitely many nonradial sign-changing solutions for N = 4 or N ⩾ 6. In any case mentioned above, the range of μ depends on the value of a: |μ| can be large if a > 0 is small.
Michael Winkler 2018 Nonlinearity 31 2031
This paper is concerned with radially symmetric solutions of the Keller–Segel system with nonlinear signal production, as given by 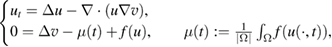 in the ball
in the ball 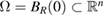 for
for 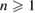 and R > 0, where f is a suitably regular function generalizing the prototype determined by the choice
and R > 0, where f is a suitably regular function generalizing the prototype determined by the choice 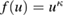 ,
, 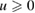 , with
, with 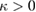 .
.
The main results assert that if in this setting the number κ satisfies  then for any prescribed mass level m > 0, there exist initial data u0 with
then for any prescribed mass level m > 0, there exist initial data u0 with 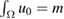 , for which the solution of the corresponding Neumann initial-boundary value problem blows up in finite time.
, for which the solution of the corresponding Neumann initial-boundary value problem blows up in finite time.
The condition in ( ) is essentially optimal and is indicated by a complementary result according to which in the case
) is essentially optimal and is indicated by a complementary result according to which in the case 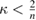 , for widely arbitrary initial data, a global bounded classical solution can always be found.
, for widely arbitrary initial data, a global bounded classical solution can always be found.
Journal links
Journal information
- 1988-present
Nonlinearity
doi: 10.1088/issn.0951-7715
Online ISSN: 1361-6544
Print ISSN: 0951-7715