Abstract
We consider a family of piecewise contractions admitting a rotation number and defined for every 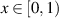 by
by 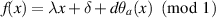 , where
, where 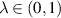 ,
, 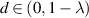 ,
, ![$\delta\in[0,1]$](https://content.cld.iop.org/journals/0951-7715/39/2/025005/revision1/nonae3b8dieqn5.gif) ,
, ![$a\in[0,1]$](https://content.cld.iop.org/journals/0951-7715/39/2/025005/revision1/nonae3b8dieqn6.gif) and
and 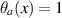 if
if 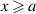 and
and 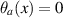 otherwise. In the special case where a = 1, the family reduces to the well studied ‘contracted rotations’
otherwise. In the special case where a = 1, the family reduces to the well studied ‘contracted rotations’ 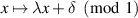 , which are 2-interval piecewise λ-affine contractions when
, which are 2-interval piecewise λ-affine contractions when 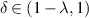 . Considering
. Considering 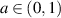 allows maps with an additional discontinuity, that is, 3-interval piecewise λ-affine contractions. Supposing λ and d fixed, for any
allows maps with an additional discontinuity, that is, 3-interval piecewise λ-affine contractions. Supposing λ and d fixed, for any 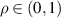 and
and ![$\alpha\in[0,1]$](https://content.cld.iop.org/journals/0951-7715/39/2/025005/revision1/nonae3b8dieqn14.gif) , we provide the values of the parameters δ and a for which the corresponding map has rotation number ρ, and a symbolic dynamics containing that of the rotation
, we provide the values of the parameters δ and a for which the corresponding map has rotation number ρ, and a symbolic dynamics containing that of the rotation 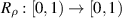 of angle ρ with respect to the partition given by the positions of
of angle ρ with respect to the partition given by the positions of 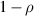 and α in
and α in 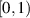 . This enables in particular to determine the maps that have a given number of periodic orbits of an arbitrary period, or a Cantor set attractor supporting a dynamics of a given complexity.
. This enables in particular to determine the maps that have a given number of periodic orbits of an arbitrary period, or a Cantor set attractor supporting a dynamics of a given complexity.
Recommended by Dr Lorenzo J Diaz