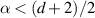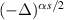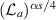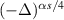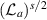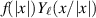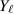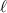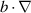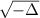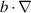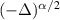Abstract
We consider the ordinary or fractional Laplacian plus a homogeneous, scaling-critical drift term. This operator is non-symmetric but homogeneous, and generates scales of Lp-Sobolev spaces which we compare with the ordinary homogeneous Sobolev spaces. Unlike in previous studies concerning Hardy operators, i.e. ordinary or fractional Laplacians plus scaling-critical scalar perturbations, handling the drift term requires an additional, possibly technical, restriction on the range of comparable Sobolev spaces, which is related to the unavailability of gradient bounds for the associated semigroup.
Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recommended by Dr David Lannes
Footnotes
- 4
- 5
- 6
We point out two misprints in [BD23, (3)]: There, the operators
and should be replaced with and , respectively. - 7
For single or finitely many eigenvalues, this is known as Feynman–Hellmann theorem.
- 8
Actually, one has to show this relative trace class condition only in every fixed angular momentum channel, i.e. when the operator is restricted to the space of square-integrable functions of the form
, where denotes the -th spherical harmonic on the unit sphere. - 9
- 10
The terminologies ‘supercritical’ and ‘critical’ are motivated by the fact that a gradient perturbation
is of the same weight as , while if α < 1, then, formally, dominates .
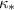
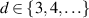
![$\alpha\in(1,2]$](https://content.cld.iop.org/journals/0951-7715/39/1/015021/revision1/nonae277aieqn69.gif)
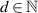
![$\alpha\in(1,2]$](https://content.cld.iop.org/journals/0951-7715/39/1/015021/revision1/nonae277aieqn71.gif)
