Multiple positive normalized solutions for nonlinear Schrödinger systems

We consider the existence of multiple positive solutions to the nonlinear Schrödinger systems set on ,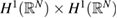

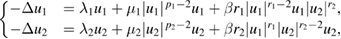
under the constraint

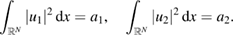
Here 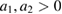are prescribed, 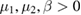, and the frequencies 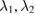are unknown and will appear as Lagrange multipliers. Two cases are studied, the first when 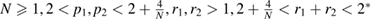, the second when 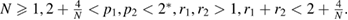In both cases, assuming that 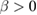is sufficiently small, we prove the existence of two positive solutions. The first one is a local minimizer for which we establish the compactness of the minimizing sequences and also discuss the orbital stability of the associated standing waves. The second solution is obtained through a constrained mountain pass and a constrained linking respectively.