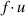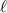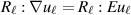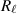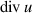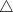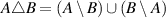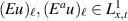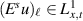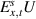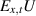Dissipation for codimension 1 singular structures in the incompressible Euler equations

We consider weak solutions to the incompressible Euler equations. It is shown that energy conservation holds in any Onsager critical class in which smooth functions are dense. The argument is independent of the specific critical regularity and the underlying PDE. This groups several energy conservation results and it suggests that critical spaces where smooth functions are dense are not at all different from subcritical ones, although possessing the ‘minimal’ regularity index. Then, we study properties of the dissipation D in the case of bounded solutions that are allowed to jump on 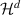-rectifiable space-time sets Σ, which are the natural dissipative regions in the compressible setting. As soon as both the velocity and the pressure possess traces on Σ, it is shown that Σ is D-negligible. The argument makes the role of the incompressibility very apparent, and it prevents dissipation on codimension 1 sets even if they happen to be densely distributed. As a corollary, we deduce energy conservation for bounded solutions of ‘special bounded deformation’, providing the first energy conservation criterion in a critical class where only an assumption on the ‘longitudinal’ increment is made, while the energy flux does not vanish for kinematic reasons.