Abstract
We present a stability result for groundstates of a Schrödinger–Poisson system in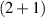 
dimension, modelling the propagation of a light beam through a liquid crystal with nonlocal nonlinear response. The core of the proof is a coercivity bound on the second derivative of the action, where non scaling nonlinearities and the coupled system present the major difficulties. In addition we prove existence of a ground state with frequency σ for any 
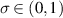as a minimal point over an appropriate Nehari manifold.
Recommended by Dr Jean-Claude Saut
Access this article
The computer you are using is not registered by an institution with a subscription to this article. Please choose one of the options below.
Login
Purchase from
Purchase this article from our trusted document delivery partners.
Make a recommendation
To gain access to this content, please complete the Recommendation Form and we will follow up with your librarian or Institution on your behalf.
For corporate researchers we can also follow up directly with your R&D manager, or the information management contact at your company. Institutional subscribers have access to the current volume, plus a 10-year back file (where available).