Trivial dynamics in discrete-time systems: carrying simplex and translation arcs

In this paper we show that the dynamical behavior in 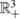(first octant) of the classical Kolmogorov systems 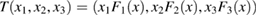of competitive type admitting a carrying simplex can be sometimes determined completely by the number of fixed points on the boundary and the local behavior around them. Roughly speaking, T has trivial dynamics (i.e. 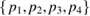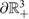the omega limit set of any orbit is a connected set contained in the set of fixed points) provided T has exactly four hyperbolic nontrivial fixed points in with 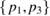local attractors on the carrying simplex and 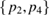local repellers on the carrying simplex; and there exists a unique hyperbolic fixed point in Int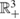. Our results are applied to some classical models including the Leslie–Gower models, Atkinson-Allen systems and Ricker maps.