Quantitative propagation of chaos for 2D viscous vortex model with general circulations on the whole space

We derive quantitative propagation of chaos in the sense of relative entropy for the 2D viscous vortex model with general circulations, approximating the vorticity formulation of the 2D Navier–Stokes equation on the whole Euclidean space. Our results work on the general setting that the vortices are positioned on the whole space 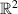and that the circulations are allowed to be in different magnitudes and orientations, which can be adapted to general unconfined realistic fluids with vorticity that may change sign. We provide explicit convergence rates which are optimal in N and optimal in t among existing literature. The key technical tools, which are our major novelty, are the sharp logarithmic growth estimates and a new ODE hierarchy and iterated integral estimates.