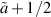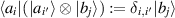Abstract
Santosh Kumar was an active researcher on the topic of exact results in random matrix theory and their various applications, particularly to quantum chaos and information theory. Barely entering his mid-career, he died unexpectedly on the 18th October 2024. The present article gives an account of some of his research directions and findings. As well as serving as a tribute to his work, this is done also for the purpose of providing a resource for those who may continue along related lines in the future.
Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Prologue
Tragedy struck for the family, friends, students and colleagues of Santosh Kumar in October last year (2024) with his sudden and unexpected death. At the time, he was working alongside, or had just graduated, several PhD students, whereby he was overseeing a steady stream of publications relating to exact results in random matrix theory (RMT). Typically these works were targeted to, or motivated by, applied domains, with quantum information, quantum chaos, telecommunications and complex systems all prominent. In addition, he was carrying out multiple lecturing and administrative duties at his home university, the Shiv Nadar Institution of Eminence, including supervising undergraduate students to provide them with a research experience. He was also collaborating internationally, with a further paper in a fruitful series of works with the present author relating to the exact computation of random matrix distribution for the classical random matrix ensembles in preparation at the time of his untimely passing.
By way of respect and appreciation for the benefit of a long standing collaboration (began in 2016, with 5 published works, one paper accepted but not yet published, and one in the refereeing process), it seems only fitting to document some of Santosh Kumar’s research finding by way of a review of aspects of his work. To give this context, some background material will also be provided. This review is ordered by various common themes where can be found in several of his works. However, as I personally do not have expertise across them all, some will not be represented. Notable among these are his research applying RMT to telecommunications (a selection of such works are [10, 12, 53, 73, 86]) and his work as a postdoc relating to the use of supersymmetry methods to analyze scattering matrix elements [52, 69]. One should draw attention to his emerging interest on aspects of non-Hermitian RMT [84, 85], which otherwise is not discussed. Also, it will not be possible to do justice to the careful numerical validation of theoretical predictions, often making use of the computer algebra software Mathematica, nor the demonstration of their applicability to model physical systems (in quantum chaos studies, the kicked top features prominently [55, 80], as do spin chains [81, 82]).
2. Quantifying entanglement
2.1. Formalism and relationship to RMT
Analytic formulas relating to a particular class of the quantum entanglement with a random matrix origin have been known in the literature for several decades now, beginning it would seem with [60, 61, 71]. The physical setting relates to the bipartite entanglement of two finite dimensional subsystems, A and B say. Let their respective dimensions be n and N, with 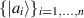 ,
, 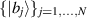 and take
and take 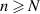 for definiteness. A general state
for definiteness. A general state 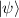 in the composite system can be written as a linear combination of the nN dimensional tensor product basis
in the composite system can be written as a linear combination of the nN dimensional tensor product basis 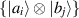 ,
,

where normalization requires

Associate with (2.1) the rectangular matrix ![$X = [x_{ij}]_{i = 1,\dots,n \atop j = 1,\dots,N}$](https://content.cld.iop.org/journals/1751-8121/58/46/463001/revision2/aae0fceieqn6.gif) . In the circumstance that
. In the circumstance that 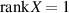 , there are bases for the subsystems
, there are bases for the subsystems 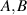 such that (2.4) decomposes as as a single tensor product of a state from subsystem A, and a state from subsystem B. In this circumstance (2.1) is said to be separable—otherwise it is entangled. A classical result from the theory of matrices gives the so-called singular value decomposition
such that (2.4) decomposes as as a single tensor product of a state from subsystem A, and a state from subsystem B. In this circumstance (2.1) is said to be separable—otherwise it is entangled. A classical result from the theory of matrices gives the so-called singular value decomposition

where U is of size n × n, L is of size n × N and V is of size N × N. In (2.3), the entries at diagonal positions (ii) (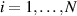 ) of L are the square root of the eigenvalues of
) of L are the square root of the eigenvalues of 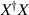 ,
, 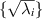 say, referred to as the singular values. According to the normalization condition (2.2) written as
say, referred to as the singular values. According to the normalization condition (2.2) written as 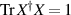 , a constraint on these eigenvalues (as well as being positive) is that
, a constraint on these eigenvalues (as well as being positive) is that 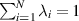 . All other entries of this matrix are zero. The rows of
. All other entries of this matrix are zero. The rows of 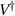 are an orthonormal basis for
are an orthonormal basis for 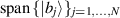 , while the columns of U are an orthonormal basis for
, while the columns of U are an orthonormal basis for 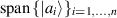 .. Let these new orthonormal bases be specified as
.. Let these new orthonormal bases be specified as 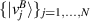 and
and 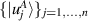 . They allow (2.2) to be simplified,
. They allow (2.2) to be simplified,

giving what is referred to as the Schmidt decomposition (see e.g. [17] in relation to the naming).
By definition, the density matrix associated with the state (2.1) of the composite system is the 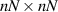 rank one matrix
rank one matrix

The reduced density matrix of subsystem B obtained by tracing out over subsystem A1,

In terms of the Schmidt decomposition (2.4) this takes the form

which one recognizes as the form of a density matrix for a statistical mixture of pure states, each state 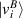 occurring with probability λi (see e.g. the recent review [7]). Moreover, from the meaning of the quantities in (2.4), one has the explicit matrix form
occurring with probability λi (see e.g. the recent review [7]). Moreover, from the meaning of the quantities in (2.4), one has the explicit matrix form

Having arrived at the formula (2.8), one would like to introduce randomness into the problem by devising an ensemble theory. This would be in keeping with the coefficients in (2.1) making up the matrix X being random, up to the constraint (2.2). Actually the requirement that X (in distribution) is unchanged by left and right conjugation by unitary matrices should also be added as a constraint, as only then will ρB be independent of the particular choice of basis in (2.1). With an eye towards exact solutions, and knowing the special role played in RMT by the Gaussian distribution from this viewpoint (see e.g. [18, 63]), one then is lead to the choice

where the n × N matrix G has independent standard complex Gaussian entries (an example of a rectangular GinUE matrix [9]). The matrix G has the bi-unitary invariant distribution proportional to 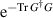 . A normalization by
. A normalization by 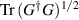 has been carried out so that X then obeys the constraint (2.2). Hence the distribution on the space of matrices X so constructed is proportional to
has been carried out so that X then obeys the constraint (2.2). Hence the distribution on the space of matrices X so constructed is proportional to 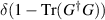 . Further, in consideration of a (rectangular) matrix X random with complex elements, it is a standard result in RMT (see e.g. [18, equation (3.23)]) that changing variables to
. Further, in consideration of a (rectangular) matrix X random with complex elements, it is a standard result in RMT (see e.g. [18, equation (3.23)]) that changing variables to 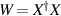 gives a Jacobian factor
gives a Jacobian factor 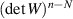 , so the distribution on W is proportional to
, so the distribution on W is proportional to

Another standard result is that changing variables from the elements of W to its eigenvalues and eigenvectors gives a Jacobian factor 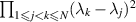 [18, equation (1.27) with β = 2]. This can be deduced from the metric on Hermitian matrices corresponding to the infinitesimal squared line element
[18, equation (1.27) with β = 2]. This can be deduced from the metric on Hermitian matrices corresponding to the infinitesimal squared line element 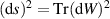 [18, section 1.2.4], which in turn corresponds to the distance function between Hermitian matrices
[18, section 1.2.4], which in turn corresponds to the distance function between Hermitian matrices

where the superscript ‘HS’ stands for Hilbert–Schmidt. Hence one is led [37, 95] to a probability density function (PDF) on the 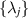 in (2.7) proportional to
in (2.7) proportional to
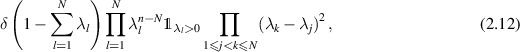
which due to its relation to (2.11) is referred to as the Hilbert–Schmidt measure for density matrices.
For 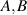 density matrices, an alternative to (2.11) is the distance function
density matrices, an alternative to (2.11) is the distance function
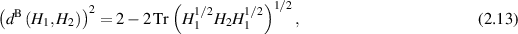
which enjoys several distinguished properties [6]. Forming a line element of a single density matrix based on this Bures distance function, it was shown by Hall [37] that the implied Jacobian for a change of variables to the eigenvalues and eigenvectors gives the Jacobian 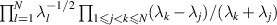 . This then gives rise to the PDF for
. This then gives rise to the PDF for 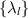 proportional to
proportional to
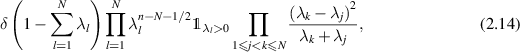
referred to as the Bures–Hall (BH) measure for density matrices. Replacing G in (2.9) by 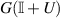 , where U is a random unitary matrix chosen with PDF proportional to
, where U is a random unitary matrix chosen with PDF proportional to 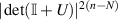 gives a realization of random density matrices with eigenvalue PDF (2.14) [25, 70].
gives a realization of random density matrices with eigenvalue PDF (2.14) [25, 70].
Scaling 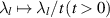 in (2.12) and (2.14) and factoring out powers of t where possible shows that the functional forms are unchanged except that
in (2.12) and (2.14) and factoring out powers of t where possible shows that the functional forms are unchanged except that 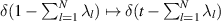 . Now multiplying by e−ts and integrating over t to form the Laplace transform then replaces this delta function term by the exponential
. Now multiplying by e−ts and integrating over t to form the Laplace transform then replaces this delta function term by the exponential 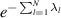 (the Laplace transform variable s can be set equal to unity by a further rescaling). The Hilbert–Schmidt measure (2.12) then becomes the eigenvalue PDF specifying the complex Wishart ensemble (or Laguerre unitary ensemble by regarding
(the Laplace transform variable s can be set equal to unity by a further rescaling). The Hilbert–Schmidt measure (2.12) then becomes the eigenvalue PDF specifying the complex Wishart ensemble (or Laguerre unitary ensemble by regarding 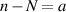 as a continuous variable), while the transformed form of (2.14) may be referred to as the Laguerre BH ensemble. In exact calculations relating to (2.12) and (2.14), it is often the case that the quantity of interest can first be deduced for its Laguerre counterpart, and then an inverse Laplace transform performed. For example, if
as a continuous variable), while the transformed form of (2.14) may be referred to as the Laguerre BH ensemble. In exact calculations relating to (2.12) and (2.14), it is often the case that the quantity of interest can first be deduced for its Laguerre counterpart, and then an inverse Laplace transform performed. For example, if 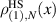 denotes the eigenvalue density for the Hilbert–Schmidt measure, and
denotes the eigenvalue density for the Hilbert–Schmidt measure, and 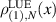 denotes the eigenvalue density for the Laguerre unitary ensemble, one has
denotes the eigenvalue density for the Laguerre unitary ensemble, one has
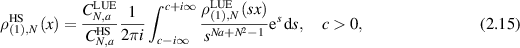
where 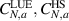 are the normalization; see e.g. [1].
are the normalization; see e.g. [1].
2.2. Some results of Kumar
2.2.1. Entanglement statistics.
Statistical quantities often used to quantify entanglement of a bipartite system as encoded in (2.7) are von Neumann entropy µvN and purity µ2 specified by
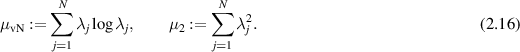
Let 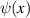 denote the digamma function. In the Hilbert–Schmidt case it has been known for a long time [36, 71, 83, 88] that
denote the digamma function. In the Hilbert–Schmidt case it has been known for a long time [36, 71, 83, 88] that
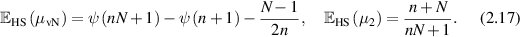
By way of interpretation, one notes that in the limit 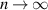 (in the bipartite formalism, n is the dimension of subsystem A), these formulas give
(in the bipartite formalism, n is the dimension of subsystem A), these formulas give 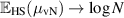 ,
, 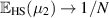 , which is to be expected as then ρB approaches
, which is to be expected as then ρB approaches 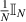 , as can be seen from its construction (2.8). Also special is the case
, as can be seen from its construction (2.8). Also special is the case 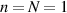 corresponding to a pure state so that ρB has a single eigenvalue, which equals unity, and thus
corresponding to a pure state so that ρB has a single eigenvalue, which equals unity, and thus 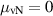 ,
, 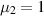 , which indeed are properties of (2.17).
, which indeed are properties of (2.17).
In [78], Sarkar and Kumar took up the problem of computing µvN and µ2 for the BH measure. Their approach was to use a known Pfaffian structure associated with the Laguerre BH ensemble [25] to obtain a computable formula for the one-point density, which was then lifted to a computable formula for the one-point density of the BH measure using (an appropriate modification of) (2.15). Noting that both quantities in (2.16) have the structure 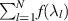 of a linear statistic, use was then made of the general formula
of a linear statistic, use was then made of the general formula
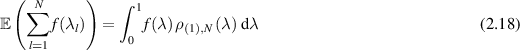
(here the fact that the eigenvalues are supported on (0, 1) has been used in the terminals of integration) to obtain the exact (rational) values of the means. Moreover, it was found that the tabulated values were consistent with the functional forms
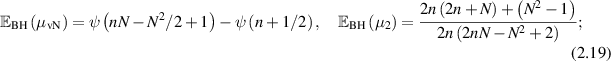
one can verify (as was done in [78]) that the consistency checks noted below (2.17) are features of these formulas. For  the first of these gives
the first of these gives 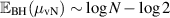 , whereas (2.16) gives
, whereas (2.16) gives 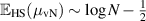 ; see also [88].
; see also [88].
The conjectures (2.19) inspired multiple works by Wei [89, 90], and Wei et al [59, 91, 92], relating to measures of entanglement with respect to the BH measure. In particular, in [89] a proof was given of (2.19). A key ingredient for this was to supplement the Pfaffian structure as already used in [78], with the explicit functional form for the eigenvalue density in terms of Meijer G-functions known from [25]. Special function properties of the Meijer G-function were then used to facilitate the evaluation of the averages as specified by (2.18). Generally, in relation to the statistical properties of a linear statistic, at the next level of complexity beyond the mean is the variance. This is given in terms of the truncated (or connected) two-point correlation 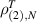 according to
according to
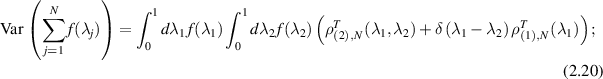
see e.g. [21, Prop. 2.1]. Beginning with (2.20), and knowledge of 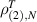 from [25], Wei [90] extended the exact result for
from [25], Wei [90] extended the exact result for 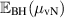 in (2.19) by deriving that
in (2.19) by deriving that
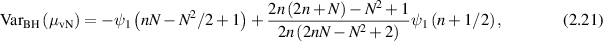
where 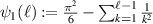 is the trigamma function. Since
is the trigamma function. Since 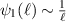 as
as 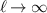 , the large N asymptotic form of (2.21) is, for
, the large N asymptotic form of (2.21) is, for 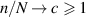 ,
, 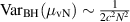 . A conjecture from [90] is the asymptotic Gaussian fluctuation formula
. A conjecture from [90] is the asymptotic Gaussian fluctuation formula

2.2.2. Density matrix distances.
The distance functions underpinning the Hilbert–Schmidt measure, and the BH measure, are (2.11) and (2.13) respectively. Construction of the density matrices for each of these measures in the form 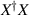 , with X specified in terms of (rectangular) standard complex Gaussian matrices has been noted in (2.9) (Hilbert–Schmidt case) and in the text below (2.14) (BH case). In the work [50], Kumar initiated the study of the distance function (2.11), with
, with X specified in terms of (rectangular) standard complex Gaussian matrices has been noted in (2.9) (Hilbert–Schmidt case) and in the text below (2.14) (BH case). In the work [50], Kumar initiated the study of the distance function (2.11), with 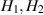 random density matrices as relate to the Hilbert–Schmidt measure, with one of the density matrices relating to a rectangular matrix of X of size
random density matrices as relate to the Hilbert–Schmidt measure, with one of the density matrices relating to a rectangular matrix of X of size 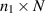 , and the other to a rectangular matrix of X of size
, and the other to a rectangular matrix of X of size 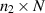 . In this setting it was shown
. In this setting it was shown
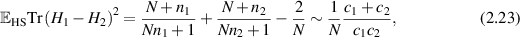
where 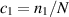 and
and 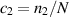 ; see also [75] in relation to the asymptotic form for
; see also [75] in relation to the asymptotic form for 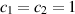 . In a subsequent work [58], Laha and Kumar extended this exact result for the mean to an exact evaluation of the corresponding variance. We make note only of its large N asymptotic form
. In a subsequent work [58], Laha and Kumar extended this exact result for the mean to an exact evaluation of the corresponding variance. We make note only of its large N asymptotic form

The works [50] and [58] also contain exact results in the case that only one of the density matrices 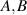 is random from the Hilbert–Schmidt measure, with the other density matrix fixed.
is random from the Hilbert–Schmidt measure, with the other density matrix fixed.
In (2.13) the quantity
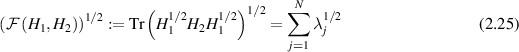
is referred to as the (square root of) the fidelity. Here 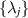 are the eigenvalues of the matrix product
are the eigenvalues of the matrix product 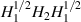 . In the case that
. In the case that 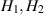 are complex Wishart matrices, and thus relate to density matrices with Hilbert–Schmidt measure but without the fixed trace constraint, in [2] the statistical state formed by the eigenvalues of such matrix products have been analyzed as examples of specific biorthogonal ensembles [8] involving Meijer G-functions. From this starting point, Laha et al [56], and Laha and Kumar [57] computed for the average square root fidelity
are complex Wishart matrices, and thus relate to density matrices with Hilbert–Schmidt measure but without the fixed trace constraint, in [2] the statistical state formed by the eigenvalues of such matrix products have been analyzed as examples of specific biorthogonal ensembles [8] involving Meijer G-functions. From this starting point, Laha et al [56], and Laha and Kumar [57] computed for the average square root fidelity
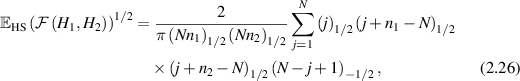
where 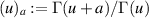 , and for the average fidelity
, and for the average fidelity
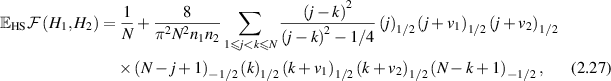
where 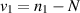 and
and 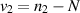 .
.
2.3. Statistics of the smallest eigenvalue
In [55], Kumar and his students pointed out that the unit trace requirement implies the constraint 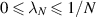 for the smallest eigenvalue. Significantly,
for the smallest eigenvalue. Significantly, 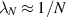 implies that all the remaining
implies that all the remaining 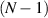 eigenvalues must similarly take a value approximately equal to
eigenvalues must similarly take a value approximately equal to 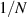 , which is the condition for (close to) maximum von Neumann entropy. Further, the other extreme
, which is the condition for (close to) maximum von Neumann entropy. Further, the other extreme 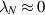 can be taken as an indicator that the effective Hilbert space dimension of the subsystem under consideration can be effectively reduced by one. These observations motivated a study of the exact computation of the distribution of the smallest eigenvalue for the Hilbert–Schmidt measure.
can be taken as an indicator that the effective Hilbert space dimension of the subsystem under consideration can be effectively reduced by one. These observations motivated a study of the exact computation of the distribution of the smallest eigenvalue for the Hilbert–Schmidt measure.
Consider first the complex Wishart ensemble, which replaces the delta function in (2.12) by an exponential. The probability of no eigenvalues in 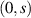 is, with
is, with 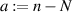
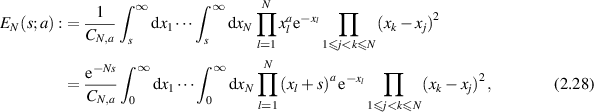
where 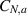 denotes the normalization. With a a non-negative integer, one sees that the multi-dimensional integral is a polynomial of degree Na in s and thus
denotes the normalization. With a a non-negative integer, one sees that the multi-dimensional integral is a polynomial of degree Na in s and thus

for some coefficients 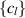 . Now let
. Now let 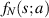 denote the PDF for the smallest eigenvalue. One has the general relation
denote the PDF for the smallest eigenvalue. One has the general relation 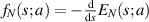 , which combined with the fact that
, which combined with the fact that 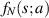 must be proportional to sa for small s gives that
must be proportional to sa for small s gives that 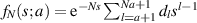 for some coefficients
for some coefficients 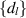 simply related to
simply related to 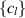 . Now let
. Now let 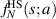 denote the smallest eigenvalue PDF for the Hilbert–Schmidt measure. By use of the inverse Laplace transform (recall (2.15) and associated text) it then follows
denote the smallest eigenvalue PDF for the Hilbert–Schmidt measure. By use of the inverse Laplace transform (recall (2.15) and associated text) it then follows
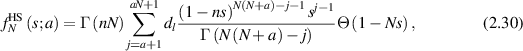
where 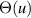 denotes the Heaviside function. Two possible ways to compute
denotes the Heaviside function. Two possible ways to compute 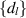 are noted in [55]. One is to make use of a known [22] determinant formula for the polynomial portion of
are noted in [55]. One is to make use of a known [22] determinant formula for the polynomial portion of 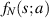 , involving an a × a Wronskian type matrix based on certain Laguerre polynomials. The other is to make use of a modification of a differential recursion scheme from the theory of Selberg integrals [3, 15], [18, section 4.6], well suited for implementation in computer algebra. With this carried out, (2.30) gives the exact functional form of
, involving an a × a Wronskian type matrix based on certain Laguerre polynomials. The other is to make use of a modification of a differential recursion scheme from the theory of Selberg integrals [3, 15], [18, section 4.6], well suited for implementation in computer algebra. With this carried out, (2.30) gives the exact functional form of 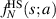 from which statistical properties of interest, for example the mean position of the smallest eigenvalue, can similarly be computed exactly.
from which statistical properties of interest, for example the mean position of the smallest eigenvalue, can similarly be computed exactly.
3. Real eigenvalues of certain integrable asymmetric random matrix ensembles and the Meijer G-function
3.1. A conjectured arithmetic property
The Meijer G-function, which has already been mentioned in passing in section 2, is defined as the particular Mellin transform
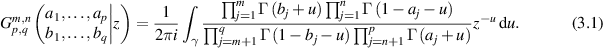
Here the contour γ goes from 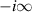 to
to 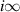 with the poles of
with the poles of 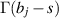 on the left and those of
on the left and those of 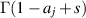 on the right; see [62] in relation to its many special properties.
on the right; see [62] in relation to its many special properties.
Our interest in this section on the Meijer G-function is its appearance in a formula for the probability, 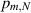 say, that all the eigenvalues in the product of m independent N × N standard real Gaussian matrices (also referred to as GinOE matrices [9]) are real. The result depends on the parity of N. With N even for definiteness, we have from [20] that
say, that all the eigenvalues in the product of m independent N × N standard real Gaussian matrices (also referred to as GinOE matrices [9]) are real. The result depends on the parity of N. With N even for definiteness, we have from [20] that
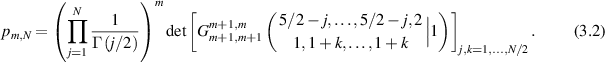
Specializing now to the case m = 2 (i.e. the product of two standard real Gaussian matrices), evidence (by way of high precision numerical evaluation) that all the entries of (3.2) are of the form π2 times a rational number, which was put forward as a conjecture. Note that the arithmetic structure of the probability of 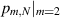 itself as a power of π times a rational number then follows as a corollary. Earlier, in [16], it had been shown that
itself as a power of π times a rational number then follows as a corollary. Earlier, in [16], it had been shown that 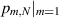 is equal to the rational number
is equal to the rational number 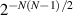 , and special arithmetic properties of the probability of some specific number k of real eigenvalues for the product of a standard real Gaussian matrix and the inverse of a standard real Gaussian matrix had been deduced [32].
, and special arithmetic properties of the probability of some specific number k of real eigenvalues for the product of a standard real Gaussian matrix and the inverse of a standard real Gaussian matrix had been deduced [32].
3.2. Kumar’s proof
The work of Kumar [47] gave a proof of the above conjecture, by deriving a closed form expression for the particular 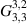 as finite sums. At the same time this provides an efficient and exact computational scheme for the entries in (3.2).
as finite sums. At the same time this provides an efficient and exact computational scheme for the entries in (3.2).
The methodology behind such formulas, presented in more generality in the subsequent work [23], is to combined the general three-term recurrence relation for Meijer G-functions [62]
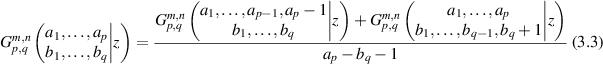
for n < p and m < q; together with evaluations [25, 62]
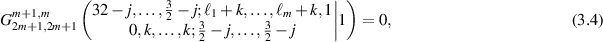
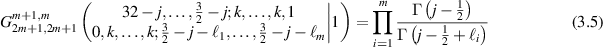
for non-negative integers 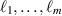 , when not all of them are 0.
, when not all of them are 0.
Through the use of (3.3)–(3.5), it was shown in [47] that
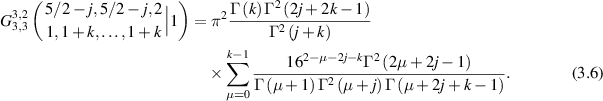
This indeed displays the arithmetic property conjectured in relation to the entries of (3.2) for m = 2.
3.3. Products of truncated orthogonal random matrices
The random matrix ensemble obtained by considering the leading N × N sub-block of an 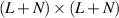 Haar distributed real orthogonal matrices has been exhibited to have special integrability properties [19, 38]. In subsequent works by Kumar and collaborators (including the present author) [23, 26] this was shown to similarly be true of products of such matrices, in which the parameter L may vary in the product. Specifically, with N even for definiteness, it was shown that
Haar distributed real orthogonal matrices has been exhibited to have special integrability properties [19, 38]. In subsequent works by Kumar and collaborators (including the present author) [23, 26] this was shown to similarly be true of products of such matrices, in which the parameter L may vary in the product. Specifically, with N even for definiteness, it was shown that
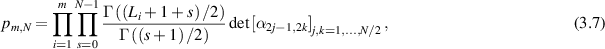
where
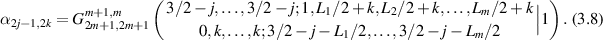
Using the recurrence (3.3) and associated boundary conditions (3.4), (3.5), a finite sum result was obtained for

where all parameters are assumed to be positive integers, as relevant to the case m = 2 with  even. In particular, this was shown to always equal a rational number, with all terms in the sum rational. In fact the recursion (3.3) can be used to establish that for any m, with
even. In particular, this was shown to always equal a rational number, with all terms in the sum rational. In fact the recursion (3.3) can be used to establish that for any m, with  even,
even, 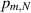 is a rational number. Specific examples with
is a rational number. Specific examples with 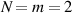 , using the notation
, using the notation 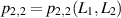 to make explicit the values of
to make explicit the values of 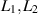 tabulated included
tabulated included
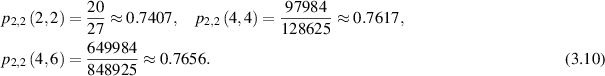
It is easy to establish at the level of the joint distribution that in the limit 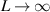 , the N × N sub-block of an
, the N × N sub-block of an 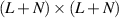 Haar distributed orthogonal random matrices, upon multiplying by
Haar distributed orthogonal random matrices, upon multiplying by 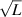 limits to a standard Gaussian random matrices. It follows that as the Li’s increase, the probability
limits to a standard Gaussian random matrices. It follows that as the Li’s increase, the probability 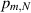 must approach that as for products of standard Gaussian random matrices. Taking this limit in (3.7), it was shown in [25] that indeed (3.2) results. For the product of two independent
must approach that as for products of standard Gaussian random matrices. Taking this limit in (3.7), it was shown in [25] that indeed (3.2) results. For the product of two independent 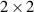 real Gaussian matrices, one has from [20, 47] that the probability of all eigenvalues being real equals
real Gaussian matrices, one has from [20, 47] that the probability of all eigenvalues being real equals 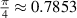 , which is in keeping with the trend seen in (3.10).
, which is in keeping with the trend seen in (3.10).
When the product involves odd Li, the arithmetic structure is more complex. For example, it was demonstrated in [26] that 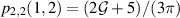 ,
, 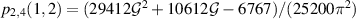 , where
, where 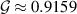 is Catalan’s constant.
is Catalan’s constant.
4. Particular biorthogonal and Pfaffian ensembles
4.1. The difference Wishart ensemble
The structure of (2.11) suggests the problem of the statistical state formed by 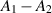 for
for 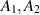 positive definite random matrices. When
positive definite random matrices. When 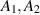 are density matrices drawn from different Hilbert–Schmidt measures, this problem was first considered in [65]. Kumar and Charan [51], for
are density matrices drawn from different Hilbert–Schmidt measures, this problem was first considered in [65]. Kumar and Charan [51], for 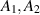 independent complex Wishart matrices, considered the generalized difference
independent complex Wishart matrices, considered the generalized difference 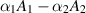 , with
, with 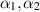 scalars. (Earlier, in [74], Kumar et al had interest in s positive weighted sum of Wishart matrices).
scalars. (Earlier, in [74], Kumar et al had interest in s positive weighted sum of Wishart matrices).
Two formalisms were applied. With 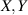 denoting N × N Hermitian matrices with eigenvalues
denoting N × N Hermitian matrices with eigenvalues 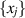 ,
, 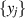 , the first was based on the matrix integral over Haar unitary matrices [42]
, the first was based on the matrix integral over Haar unitary matrices [42]
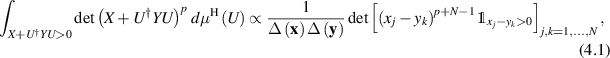
where with 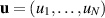 ,
, 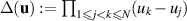 . The second made use of what is known as the derivative principle [11, 43, 93]
. The second made use of what is known as the derivative principle [11, 43, 93]

where 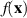 on the LHS refers to the joint eigenvalue PDF of a unitary invariant Hermitian matrix ensemble,
on the LHS refers to the joint eigenvalue PDF of a unitary invariant Hermitian matrix ensemble, 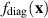 on the RHS refers to the joint eigenvalue PDF of the diagonal entries,
on the RHS refers to the joint eigenvalue PDF of the diagonal entries, 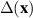 is as in (4.1) and
is as in (4.1) and 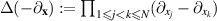 .
.
The two approaches give rise to (different) biorthogonal ensemble structures for the joint eigenvalue PDF. In the case of the use of the derivative principle, the joint eigenvalue PDF exhibits the additional structure of a polynomial ensemble [44, 46]. This permitted the general k-point correlation function to be expressed in terms of a certain correlation kernel (albeit which itself involves N × N determinants). Independent of these structures, but based instead on methods from free probability theory [76], an exact functional form of the global density, involving cube and square roots, was obtained.
4.2. Combinations of complex Wishart and Gaussian unitary ensemble(GUE) matrices
Let W be a complex Wishart matrix (Laguerre unitary ensemble—LUE) with Laguerre parameter 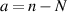 , and let G be an N × N matrix from the GUE. In [48] Kumar considered the eigenvalues for the unitary invariant ensemble specified by
, and let G be an N × N matrix from the GUE. In [48] Kumar considered the eigenvalues for the unitary invariant ensemble specified by

A matrix integral approach was used to obtain an explicit polynomial ensemble form for the joint eigenvalue PDF, i.e. having the form

for some 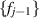 . The subsequent work [45] (see also [39]) highlights that for all random matrix sums X + Y, where
. The subsequent work [45] (see also [39]) highlights that for all random matrix sums X + Y, where 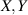 are independent polynomial ensembles, there is a systematic approach using the theory of spherical transforms and spherical functions as introduced into RMT (in the context of unitary invariant products) in [40, 41]. In particular, when one member of the sum is a GUE matrix, scaled so that the diagonal entries are standard Gaussians, and the other a general polynomial ensemble (4.4) (scaled so that the diagonal entries are standard Gaussians) the sum remains a polynomial ensemble, specifically with
are independent polynomial ensembles, there is a systematic approach using the theory of spherical transforms and spherical functions as introduced into RMT (in the context of unitary invariant products) in [40, 41]. In particular, when one member of the sum is a GUE matrix, scaled so that the diagonal entries are standard Gaussians, and the other a general polynomial ensemble (4.4) (scaled so that the diagonal entries are standard Gaussians) the sum remains a polynomial ensemble, specifically with
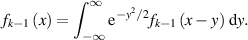
Also considered by Kumar in [48] were the eigenvalues of the product WG. After decomposing 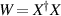 for X an n × N (
for X an n × N (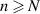 ) rectangular standard complex Gaussian matrix, the problem becomes one of studying the eigenvalues of
) rectangular standard complex Gaussian matrix, the problem becomes one of studying the eigenvalues of 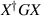 . Now replace G by any polynomial ensemble (4.4). It was shown in [24] that the joint eigenvalue PDF of this random product is proportional to
. Now replace G by any polynomial ensemble (4.4). It was shown in [24] that the joint eigenvalue PDF of this random product is proportional to
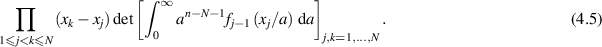
An important intermediate step in establishing (4.5) is to determine the eigenvalue PDF for the random product 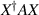 , where A is a fixed Hermitian matrix with a prescribed number of negative eigenvalues. For this purpose, one of the methods given in [24] was to make use of a pseudo-unitary group generalization of the celebrated Harish–Chandra/Itzykson–Zuber matrix integral [34, 35]
, where A is a fixed Hermitian matrix with a prescribed number of negative eigenvalues. For this purpose, one of the methods given in [24] was to make use of a pseudo-unitary group generalization of the celebrated Harish–Chandra/Itzykson–Zuber matrix integral [34, 35]
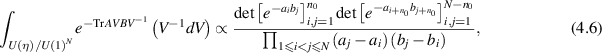
where the ai (bi) are the ordered eigenvalues of A (B), with exactly n0 of each negative. Here, with 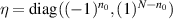 (here the notation
(here the notation 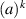 denotes a repeated k times),
denotes a repeated k times), 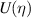 denotes the set of N × N pseudo unitary matrices specified by the requirement that
denotes the set of N × N pseudo unitary matrices specified by the requirement that 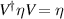 .
.
4.3. Pandey–Mehta crossover ensemble
Introduce a weighted sum of N × N real symmetric matrices from the Gaussian orthogonal ensemble (GOE; see [18, section 1.2]), and a complex Hermitian matrix from the GUE according to

In [64, 72] the joint eigenvalue PDF was computed as proportional to
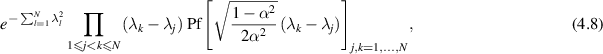
valid for N even, while for N odd the size of the determinant must be increased by one, with the final column all entries 1 except the last which is 0, and the final row all entries −1 except for the last which must be zero to match the final column.
In [79] Kumar and his students took up the task of computing the distribution of the ratio statistic 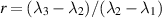 in the case N = 3. For the N = 3 GOE and GUE ensembles the exact evaluation of this statistic (with corresponding PDF
in the case N = 3. For the N = 3 GOE and GUE ensembles the exact evaluation of this statistic (with corresponding PDF 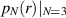 say) has been carried out earlier in [4], and shown to be an accurate approximation to the
say) has been carried out earlier in [4], and shown to be an accurate approximation to the 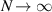 limit of this distribution (in relation to the latter, see the recent work [68]). These results were shown to be special cases of the crossover ensemble result
limit of this distribution (in relation to the latter, see the recent work [68]). These results were shown to be special cases of the crossover ensemble result
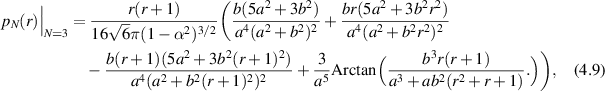
where 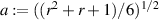 ,
, 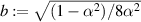 (take α → 0 for the GOE result, and α → 1 for the GUE). Starting from this form, it is shown in [79] that the general fractional moment
(take α → 0 for the GOE result, and α → 1 for the GUE). Starting from this form, it is shown in [79] that the general fractional moment 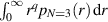 can be evaluated as a single integral involving the Tricomi function (confluent hypergeometric function of the second kind).
can be evaluated as a single integral involving the Tricomi function (confluent hypergeometric function of the second kind).
Another study by Kumar and his students [77] relating to the crossover ensemble (4.7) sought to quantify the multifractal dimension of the eigenvectors. Required for this purpose was the exact distribution of a generic eigenvector component. The latter (PDF 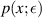 say, with
say, with 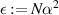 ) was given exactly in [87] as a certain double integral. In [77] it was shown that one of the integral over one of the variables therein can be computed in closed form, with the simplified exact result reading
) was given exactly in [87] as a certain double integral. In [77] it was shown that one of the integral over one of the variables therein can be computed in closed form, with the simplified exact result reading
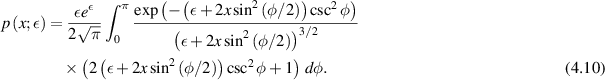
5. Quantum conductance statistic
5.1. Formalism
The quantum conductance problem relates to a mesoscopic wire of length much smaller than the coherence length, but much larger than the mean free path, as distinguishes the metallic phase [66]. At each end the wire is connected to electron reservoirs of different chemical potentials, creating a current. The quantity of interest is the dimensionless conductance 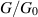 , where
, where 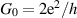 is twice the fundamental quantum unit of conductance.
is twice the fundamental quantum unit of conductance.
It is assumed that at the left (right) end the wire permits n (N) channels, with 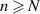 for convenience (channels are the plane wave states distinguished by their wavenumber). Associated with these states are the 2n components vector
for convenience (channels are the plane wave states distinguished by their wavenumber). Associated with these states are the 2n components vector 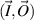 (left end) and the 2N component vector
(left end) and the 2N component vector 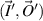 (right end). Here
(right end). Here 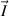 (
(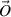 ) and
) and 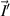 (
(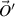 ) denote the n (N) component amplitude of the plane wave states traveling into (out of) the left and right ends of the wire. Flux conservation requires that
) denote the n (N) component amplitude of the plane wave states traveling into (out of) the left and right ends of the wire. Flux conservation requires that 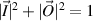 . The
. The 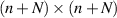 size unitary matrix S relating the flux traveling into the wire from either end, to the flux traveling out according to
size unitary matrix S relating the flux traveling into the wire from either end, to the flux traveling out according to
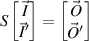
is referred to as the scattering matrix. Further, it is convenient to decompose S into blocks relating to the reflection and transmission of the current according to
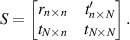
A key formula—referred to as the Landauer formula—gives for the dimensionaless conductance (see e.g. [5])

where in the second equality 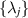 refers to the eigenvalues of
refers to the eigenvalues of 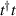 .
.
In the case of perfect leads between the wire and the reservoirs it is hypothesized that S is well described by an 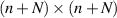 random Haar distributed unitary. Hence, according to (5.1), the question becomes to specify the distribution of the squared singular values of an N × N sub-block on the such a Haar unitary. It was deduced in [5, 67] that this is specified by the PDF proportional to
random Haar distributed unitary. Hence, according to (5.1), the question becomes to specify the distribution of the squared singular values of an N × N sub-block on the such a Haar unitary. It was deduced in [5, 67] that this is specified by the PDF proportional to

where 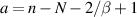 and β = 2 (if there is no time reversal symmetry the scattering matrix should belong to Dyson’s circular orthogonal ensemble of symmetric unitary matrices—see [18, section 2.2.2] — of size
and β = 2 (if there is no time reversal symmetry the scattering matrix should belong to Dyson’s circular orthogonal ensemble of symmetric unitary matrices—see [18, section 2.2.2] — of size 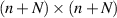 and the PDF for the squared singular values of an N × N sub-block is given by (5.2) with β = 1). Replacing each
and the PDF for the squared singular values of an N × N sub-block is given by (5.2) with β = 1). Replacing each 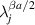 by
by 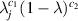 the corresponding PDF specifies the Jacobi β ensemble with Jacobi parameters
the corresponding PDF specifies the Jacobi β ensemble with Jacobi parameters 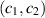 — thus the Jacobi parameters in (5.2) are
— thus the Jacobi parameters in (5.2) are 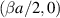 .
.
Referring back to (5.1) one has 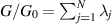 , and so also has the interpretation as the trace statistic for particular Jacobi β ensembles. The PDF for the trace statistic is obtained by averaging
, and so also has the interpretation as the trace statistic for particular Jacobi β ensembles. The PDF for the trace statistic is obtained by averaging 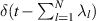 against the PDF for the Jacobi β ensemble. Taking the Laplace transform of this average (using the scaled Laplace variable
against the PDF for the Jacobi β ensemble. Taking the Laplace transform of this average (using the scaled Laplace variable 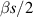 for later convenience) gives now the Jacobi β ensemble average of
for later convenience) gives now the Jacobi β ensemble average of 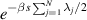 . In the case of Jacobi parameters
. In the case of Jacobi parameters 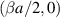 , changing variables
, changing variables 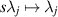 shows that up to normalization this new average can be written
shows that up to normalization this new average can be written
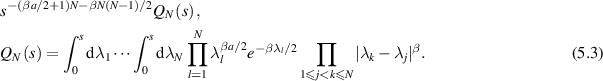
The multiple integral 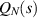 has an interpretation in RMT quite distinct from the trace statistic of a class of Jacobi β ensembles. Thus, up to normalization, it specifies the probability that there are no eigenvalues in the interval
has an interpretation in RMT quite distinct from the trace statistic of a class of Jacobi β ensembles. Thus, up to normalization, it specifies the probability that there are no eigenvalues in the interval 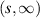 of the Laguerre β ensemble (specific Laguerre weight
of the Laguerre β ensemble (specific Laguerre weight 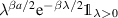 ). The derivative of this probability with respect to s gives the distribution of the largest eigenvalue. In the case β = 2, the distribution of the smallest eigenvalue in this same ensemble occurred in the context of the Hilbert–Schmidt measure. One recalls from section 2.3 that there the special structure (2.29) for a a non-negative integer facilitated the computation of the required inverse Laplace transform. To make use of (5.3) for purposes of computing the PDF of the particular Jacobi β ensemble trace statistic (or equivalently the dimensionless conductance), it is also necessary to be able to express
). The derivative of this probability with respect to s gives the distribution of the largest eigenvalue. In the case β = 2, the distribution of the smallest eigenvalue in this same ensemble occurred in the context of the Hilbert–Schmidt measure. One recalls from section 2.3 that there the special structure (2.29) for a a non-negative integer facilitated the computation of the required inverse Laplace transform. To make use of (5.3) for purposes of computing the PDF of the particular Jacobi β ensemble trace statistic (or equivalently the dimensionless conductance), it is also necessary to be able to express 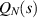 in a form that permits the computation of the inverse Laplace transform.
in a form that permits the computation of the inverse Laplace transform.
5.2. Some findings of Kumar
5.2.1. Recursive computation.
In the first of several works on the functional form and computation of the distribution of the ordered eigenvalues for classical ensembles joint with the present author [27–31], Kumar [27] took up this problem. It was observed that for 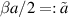 a non-negative integer, and β a positive integer,
a non-negative integer, and β a positive integer, 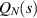 permits an evaluation that like (2.29) only involves exponentials and powers,
permits an evaluation that like (2.29) only involves exponentials and powers,

for some coefficients 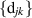 . After multiplication by the power of s as required by (5.3), this indeed then permits the computation of the required inverse Laplace transform to be calculated. Thus with
. After multiplication by the power of s as required by (5.3), this indeed then permits the computation of the required inverse Laplace transform to be calculated. Thus with 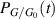 denoting the PDF of the dimensionless conductance, direct calculation then shows
denoting the PDF of the dimensionless conductance, direct calculation then shows
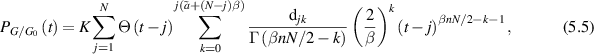
where 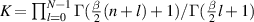 cf (2.30). Underlying (5.4) are the facts that for β an even positive integer, the product over pairs in (5.3) expands to a multivariable polynomial, and similarly for β an odd positive integer with the ordering
cf (2.30). Underlying (5.4) are the facts that for β an even positive integer, the product over pairs in (5.3) expands to a multivariable polynomial, and similarly for β an odd positive integer with the ordering  , combined with the one-dimensional integral evaluation
, combined with the one-dimensional integral evaluation
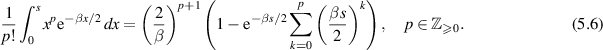
While such direct computation furthermore gives the explicit coefficients 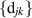 in (5.4), it is not at all efficient, being restricted for practical purposes to small β,
in (5.4), it is not at all efficient, being restricted for practical purposes to small β, 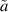 and N. A key finding in [27] is that there is a systematic recursive procedure, well suited to implementation using computer algebra, for the generation of the functional form (5.4) which is far more efficient.
and N. A key finding in [27] is that there is a systematic recursive procedure, well suited to implementation using computer algebra, for the generation of the functional form (5.4) which is far more efficient.
This requires generalizing 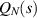 to the family of integrals
to the family of integrals
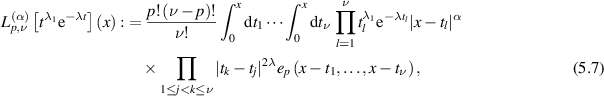
where 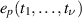 are the elementary symmetric polynomials. We have that
are the elementary symmetric polynomials. We have that
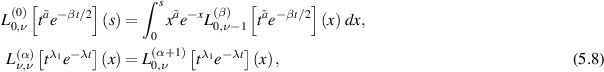
and moreover $](https://content.cld.iop.org/journals/1751-8121/58/46/463001/revision2/aae0fceieqn196.gif) . To be able to make use of the second relation in (5.8) requires a recurrence in p for the integrals (5.7), which starts with knowledge of
. To be able to make use of the second relation in (5.8) requires a recurrence in p for the integrals (5.7), which starts with knowledge of 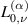 , and permits the successive computation of
, and permits the successive computation of 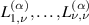 . In fact, using the abbreviated notation
. In fact, using the abbreviated notation $](https://content.cld.iop.org/journals/1751-8121/58/46/463001/revision2/aae0fceieqn199.gif) , for this purpose one has available the differential-difference second order recurrence [33, 49]
, for this purpose one has available the differential-difference second order recurrence [33, 49]
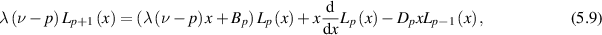
to be iterated for 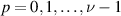 , where
, where
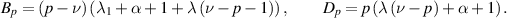
When the value 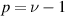 is reached and we have available
is reached and we have available 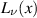 for a given α, the second relation in (5.8) can be applied. This must be done for each
for a given α, the second relation in (5.8) can be applied. This must be done for each 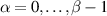 . Then ν is incremented by making use of the first recurrence in (5.8), where for this to be practical we must be able to compute the integral on the RHS. For this, the integrand having a structure of the form in (5.4) is essential.
. Then ν is incremented by making use of the first recurrence in (5.8), where for this to be practical we must be able to compute the integral on the RHS. For this, the integrand having a structure of the form in (5.4) is essential.
As an explicit example, from the implementation of the above recurrence scheme for the computation of 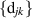 in (5.4) (there is computer algebra software associated with [27] for this purpose), substitution in (5.5) gives that
in (5.4) (there is computer algebra software associated with [27] for this purpose), substitution in (5.5) gives that
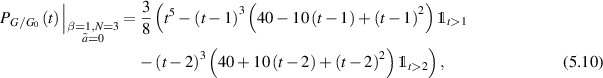
supported on 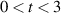 . Actually the recursive generation of this result served as a test of the method, as it was already obtained in the PhD study of Kumar (joint with his supervisor Pandey) [54], where the methodology to obtain the coefficients
. Actually the recursive generation of this result served as a test of the method, as it was already obtained in the PhD study of Kumar (joint with his supervisor Pandey) [54], where the methodology to obtain the coefficients 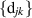 in (5.4) relied on the underlying Pfaffian structure for β = 1. Exact evaluations of
in (5.4) relied on the underlying Pfaffian structure for β = 1. Exact evaluations of 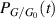 for
for 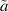 a non-negative integer, N small, and β = 4 were also carried out using a different underlying Pfaffian structure, and for β = 2 using the underlying determinant structure; cf the text below (2.30).
a non-negative integer, N small, and β = 4 were also carried out using a different underlying Pfaffian structure, and for β = 2 using the underlying determinant structure; cf the text below (2.30).
5.2.2. Matrix differential equation.
For the Jacobi β ensemble with weight 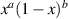 the PDF of the trace statistic
the PDF of the trace statistic 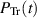 say can, for b a non-negative integer, be expressed as
say can, for b a non-negative integer, be expressed as
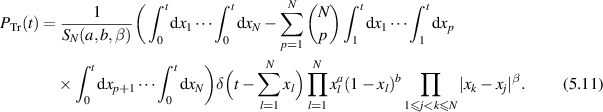
Here 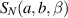 is the Selberg integral [18, section 4.1] which gives the normalization for the Jacobi β ensemble PDF. The significance of (5.11) is that due to the delta function constraint, the support of the pth term is
is the Selberg integral [18, section 4.1] which gives the normalization for the Jacobi β ensemble PDF. The significance of (5.11) is that due to the delta function constraint, the support of the pth term is 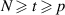 and the support of the integration variable
and the support of the integration variable 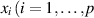 ) is
) is 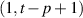 , and that of
, and that of 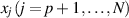 is
is 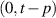 . Taking this into consideration, and restricting too to β a positive integer, working in [28] shows
. Taking this into consideration, and restricting too to β a positive integer, working in [28] shows
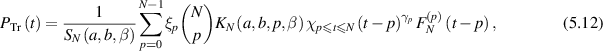
where 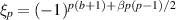 and each
and each 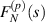 is analytic in the range
is analytic in the range 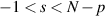 , normalized so that
, normalized so that 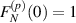 . For a a non-negative integer
. For a a non-negative integer 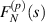 is in fact a polynomial in s of degree
is in fact a polynomial in s of degree 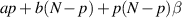 . With
. With 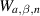 denoting the normalization for the Laguerre β ensemble with Laguerre weight
denoting the normalization for the Laguerre β ensemble with Laguerre weight 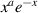 and n eigenvalues, the explicit value of
and n eigenvalues, the explicit value of 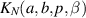 is given in [28] as
is given in [28] as 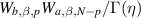 , for η a particular function quadratic in
, for η a particular function quadratic in 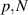 and linear in
and linear in 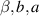 . As an illustration, the appropriate specialization of (5.12) was checked to be consistent with (5.10).
. As an illustration, the appropriate specialization of (5.12) was checked to be consistent with (5.10).
Another finding in [28] is that for a a non-negative integer, when each 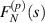 is a polynomial in s normalized to unity at s = 0, the polynomial can be computed in terms of the Frobenius type series expansion about a particular singular point of the matrix differential equation satisfied by a particular vector solution, with
is a polynomial in s normalized to unity at s = 0, the polynomial can be computed in terms of the Frobenius type series expansion about a particular singular point of the matrix differential equation satisfied by a particular vector solution, with 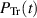 as a component. To obtain the matrix differential equation, one must first note that the differential-difference system satisfied by the Laplace transform of the trace statistic (this is essentially (5.9)) can itself be identified with a first order matrix differential equation. For example, in relation to (5.9) with ν = 3, the latter reads
as a component. To obtain the matrix differential equation, one must first note that the differential-difference system satisfied by the Laplace transform of the trace statistic (this is essentially (5.9)) can itself be identified with a first order matrix differential equation. For example, in relation to (5.9) with ν = 3, the latter reads
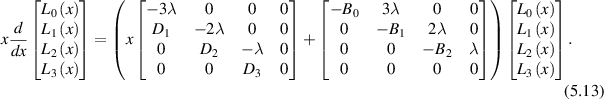
Taking the inverse Laplace transform of this—a strategy which has its origin in [13] — gives the sought matrix differential equation relating to 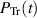 .
.
5.2.3. Structure of the conductance statistic for β = 1 and  a non-negative integer.
a non-negative integer.
In the definition of a below (5.2), one sees that with respect to the underlying matrix parameter n − N, in the case β = 1 the exponent 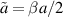 can take on half integer values, starting at
can take on half integer values, starting at 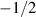 . With
. With 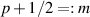 a non-negative integer, the analogue of (5.6) is
a non-negative integer, the analogue of (5.6) is
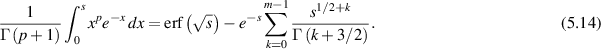
Now ordering the eigenvalues 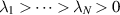 , expanding the product of differences in (5.3) as a multivariable polynomial, and applying (5.14) to compute the integral over
, expanding the product of differences in (5.3) as a multivariable polynomial, and applying (5.14) to compute the integral over 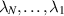 in order gives a finite sum analogous to (5.4), but with the added complication that each exponential may also involve a factor involving powers of
in order gives a finite sum analogous to (5.4), but with the added complication that each exponential may also involve a factor involving powers of 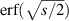 .
.
Remarkably, computer algebra implementation of the recursive algorithm of section 5.2.1 in the case β = 1 and 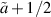 a non-negative integer carried out in [30] indicate a much simpler structure, with all higher powers of
a non-negative integer carried out in [30] indicate a much simpler structure, with all higher powers of 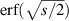 canceling out at each recursive step. It is found for low order cases with N odd that
canceling out at each recursive step. It is found for low order cases with N odd that
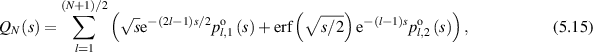
for polynomials 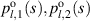 ; specifically
; specifically 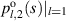 is a constant. Similarly, for N even the computer algebra implementation of the recursive algorithm indicates
is a constant. Similarly, for N even the computer algebra implementation of the recursive algorithm indicates
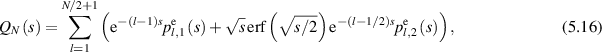
again for polynomials 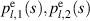 with
with 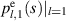 a constant.
a constant.
The significance of the structures (5.15) and (5.16) is that the inverse Laplace transform as required for the computation of of 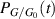 can be carried out explicitly. This would not be the case if there were higher powers of
can be carried out explicitly. This would not be the case if there were higher powers of 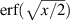 present. In particular, these findings give an explanation (and alternative derivation) for the earlier results of Kumar in [54] relating to explicit functional forms in the case β = 1 and
present. In particular, these findings give an explanation (and alternative derivation) for the earlier results of Kumar in [54] relating to explicit functional forms in the case β = 1 and 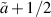 a non-negative integer deduced from the Pfaffian structure, for example
a non-negative integer deduced from the Pfaffian structure, for example
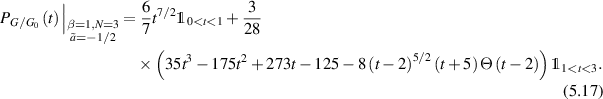
Acknowledgments
This work has been supported by the Australian Research Council discovery project grant DP250102552. Feedback on this article from Sunidhi Sen and Gustavo Fraidenraich is much appreciated, as is that of the referees.
Data availability statement
No new data were created or analysed in this study.
Footnotes
- 1
Here there is an abuse of notation; one requires that
 .
.