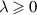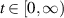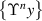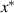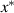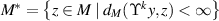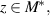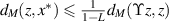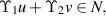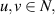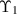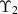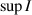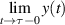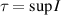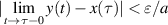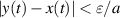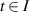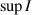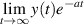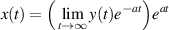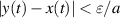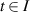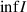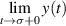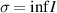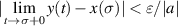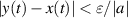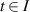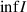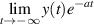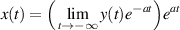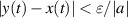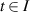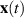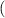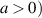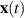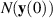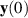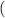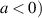Abstract
Stability theory plays a central role in the analysis of the behaviour of a solution of a real-order differential equations. In the literature, various stability concepts were introduced from the application point of view. The most popular ones are the Lyapunov and the Ulam-Hyers stability. Here, we first we establish a relation between the Lyapunov and Ulam-Hyers stability concepts for a dynamical system and prove that the concept of Ulam-Hyers is more general than that of Lyapunov. Second, we present a brief overview of recent developments in the Ulam-Hyers stability analysis of fractional-order differential equations (FDEs). These equations include linear FDEs, non-linear FDEs, delay FDEs, fractional-order boundary value problems and impulsive FDEs.
Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In 1940, Ulam introduced the following problem regarding the stability of the group homomorphism in a metric group 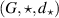 [70] where
[70] where  represents the operation in the given group G. For a given function
represents the operation in the given group G. For a given function 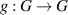 and a positive number ε satisfying
and a positive number ε satisfying
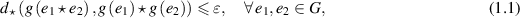
does there exist a positive constant L and a homomorphism 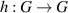 of the group (i.e.
of the group (i.e. 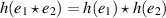 ) with the property
) with the property

If such a constant L exists that satisfies equation (1.2), then we say that the equation of the homomorphism

on the metric group is stable in the Ulam sense. A year later, Hyer provided an answer to Ulam’s problem for additive functions on Banach spaces as follows [31]:
For real Banach spaces 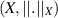 and
and 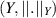 ; given a function
; given a function  and a positive number ε satisfying
and a positive number ε satisfying
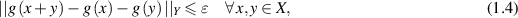
there exists a unique additive function 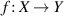 i.e.
i.e. 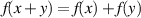 satisfying
satisfying

Such a type of stability concept is known as Ulam-Hyers stability (also Hyers-Ulam or Ulam stability). Generally speaking, a functional equation is said to be Ulam-Hyers stable, if for every solution of the perturbed equation (called approximate solution), there exists a solution of the equation (exact solution) near to it. After the Hyers result on stability many researchers have extended the concept of Ulam-Hyers stability to other functional equations, we refer the reader to [12, 13, 32, 33, 55, 58].
In 1978, Rassias [56] generalised the stability result of Hyers, an approach known as the Ulam-Hyers-Rassias stability. The stability result of Rassias is contained in the following theorem.
Theorem 1.1 ([56]). Consider 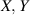 to be two Banach spaces, and let
to be two Banach spaces, and let 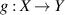 be a mapping such that f(tx) is continuous in t for each fixed x. Assume that there exists θ > 0 and
be a mapping such that f(tx) is continuous in t for each fixed x. Assume that there exists θ > 0 and 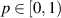 such that
such that
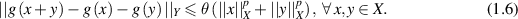
Then, there exists a unique linear mapping 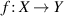 such that
such that
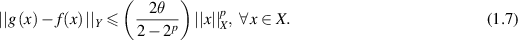
The positive number L in Ulam’s problem is called a Ulam-Hyers constant corresponding to the considered equation (1.3). Let us denote LM the infimum of all Ulam-Hyers constants L. In general LM may not be a Ulam-Hyers constant for a given functional equation (see [26]). In case when LM is an Ulam-Hyers constant it is called the best Ulam-Hyers constant. The best Ulam-Hyers constant has a major significance in the analysis of the Ulam-Hyers stability of a given functional equation. This is, because one can not only estimate the possible minimum distance between the approximate and the exact solution of the functional equation, but, at the same time, also get away with searching for other possible Ulam-Hyers constants by different approaches. For instance, Onitsuka and Shoji [52] studied the Ulam-Hyers stability of the first-order linear differential equation

where a is a non-zero real number and evaluated the best Ulam-Hyers constant 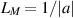 . Now, there is no interest in studying the Ulam-Hyers stability of the above problem (1.8) because whatever different approach we pursue, it will always end up with a Ulam-Hyers constant
. Now, there is no interest in studying the Ulam-Hyers stability of the above problem (1.8) because whatever different approach we pursue, it will always end up with a Ulam-Hyers constant 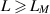 and thus will be a bad estimation of the bound for the distance between the approximate and the exact solution of equation (1.8). Finding the best Ulam-Hyers constant, if exists, for a given functional equations is a challenging task, except for some linear functional equations—finding the best Ulam-Hyers constant for non-linear functional equations is still an open problem. However, if the given functional equation does not possess the best Ulam-Hyers constant or one is unable to find the best Ulam-Hyers constant, then one can apply different approaches to improve the estimation for the Ulam-Hyers constant L.
and thus will be a bad estimation of the bound for the distance between the approximate and the exact solution of equation (1.8). Finding the best Ulam-Hyers constant, if exists, for a given functional equations is a challenging task, except for some linear functional equations—finding the best Ulam-Hyers constant for non-linear functional equations is still an open problem. However, if the given functional equation does not possess the best Ulam-Hyers constant or one is unable to find the best Ulam-Hyers constant, then one can apply different approaches to improve the estimation for the Ulam-Hyers constant L.
In a number of practical problems, integral-order derivatives and differential Equations do not convey the full picture of the situation. In many complex systems, the use of the concept of fractional-order calculus [15, 24, 29, 36, 42, 44, 47–49, 51, 54, 65] or fractional Brownian motion [6, 9, 25, 35, 43, 46, 71] offers new ways to tackle these problems Fractional-order differintegral operators incorporate long-range memory effects in terms of power-law kernels. For instance, fractional-order, linear dynamic equations can be derived from continuous time random walk processes based on scale-free sojourn time densities in the hydrodynamic limit [47, 48]. Fractional differential equations (FDEs) of different types (e.g. linear and non-linear) will be considered in the following.
The study of real-order differential equations is mainly divided into two parts: quantitative and qualitative theory. The qualitative theory is considerably more effective than the quantitative theory in the analysis of real-order differential Equations. The analysis of the qualitative properties of such differential Equations is of high interest since differential equations arise in nearly all disciplines of science, medicine, engineering, economics, demography, geophysics, and biocenology. The qualitative theory deals with diverse topics along with their physical existence, such as stability, asymptotic stability, periodic orbit, limit cycles, and chaos. Stability theory is one of the oldest and most effective concepts to analyse the dynamics of differential equations and to design control in numerous complex engineering problems. In the literature, depending upon the requirement to handle the mathematical difficulty and from an application point of view, various stability concepts have been introduced to analyse the behaviour of some of the physical states connected to the real-order differential equations. As mentioned, these include the Ulam-Hyers, Ulam-Hyers-Rassias, and Lyapunov stability, inter alia. In the case of integer-order dynamical systems the Lyapunov stability theory is a very mature subject and has a very rich mathematical foundation [34, 72]. However, over the last few decades, a good amount of research has been carried out on the applications of Lyapunov stability for fractional-order dynamical systems to more realistic problems in science and engineering [7, 67, 68]. For detailed discussion on Lyapunov stability results for FDEs we refer to the survey paper [40]. In what follows, we present different methods in a survey on the Ulam-Hyers stability results for various classes of FDEs.
The remainder of this paper is organised as follows. Section 2 introduces basic notations, definitions, and preliminary results for FDE stability analysis. Section 3 presents the concept of strong Ulam-Hyers stability and gives its relationship with Lyapunov stability in dynamical systems. Section 4 discusses Ulam-Hyers stability results of linear FDEs, while section 5 examines the nonlinear case. Section 6 deals with the Ulam-Hyers stability conditions of FDEs with delay. In section 7, we present Ulam-Hyers stability conditions of fractional boundary value problems. In section 8, we show the Ulam-Hyers stability results of fractional impulsive differential Equations are described. Finally, section 9 displays concluding remarks.
2. Preliminaries
In this section, we introduce some definitions and results, which will be used throughout this work.
Let  and
and 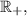 denote the set of complex numbers, the set of real numbers, the set of natural numbers, and the set of positive real numbers, respectively. Furthermore, let
denote the set of complex numbers, the set of real numbers, the set of natural numbers, and the set of positive real numbers, respectively. Furthermore, let 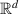 (
(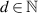 ) denote the d-dimensional Euclidean space.
) denote the d-dimensional Euclidean space.
Definition 2.1 ([54]). The Euler gamma function 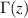 is defined by the integral
is defined by the integral

which converges in the right half of the complex plane, 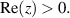
Definition 2.2 ([54]). The classical Mittag–Leffler function is the generalisation of the exponential function. The one-parameter Mittag–Leffler function Eα and two-parameter (generalised) Mittag–Leffler function 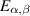 are defined, respectively, by
are defined, respectively, by
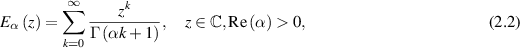
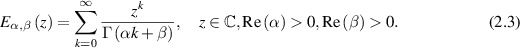
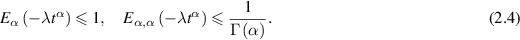
Definition 2.3 ([54]). The Riemann–Liouville fractional integral 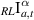 of order α > 0 of a given function v(t) is defined by
of order α > 0 of a given function v(t) is defined by
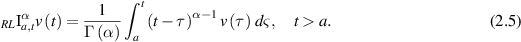
Definition 2.4 ([54]). The Riemann–Liouville fractional derivative 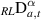 of order α > 0 of a given function v(t) is defined by
of order α > 0 of a given function v(t) is defined by
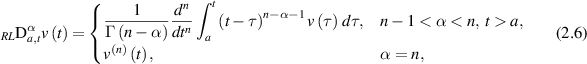
where 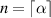 is a positive integer; here
is a positive integer; here 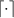 denotes the ceiling function.
denotes the ceiling function.
Definition 2.5 ([54]). The Caputo fractional derivative 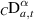 of order α > 0 of a given function v(t) is defined by
of order α > 0 of a given function v(t) is defined by
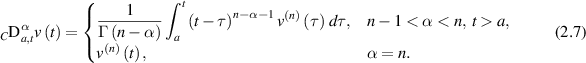
where 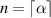 is a positive integer, and
is a positive integer, and 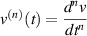 .
.
Definition 2.6 ([19]). For ![$\rho\in(0,1]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn33.gif) and α > 0. 0. The generalised proportional fractional integral
and α > 0. 0. The generalised proportional fractional integral 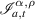 of order α > 0 of a given function v(t) is defined by
of order α > 0 of a given function v(t) is defined by
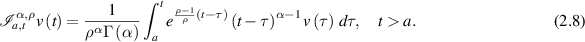
Definition 2.7 ([19]). For ![$\rho\in (0,1]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn35.gif) and
and 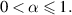 0. The generalised proportional fractional derivative of Riemann–Liouville type
0. The generalised proportional fractional derivative of Riemann–Liouville type 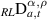 of order α of a given function v(t) is defined by
of order α of a given function v(t) is defined by
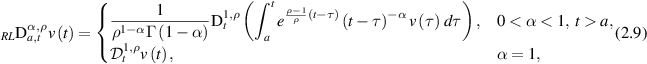
where 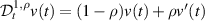 .
.
Integral inequalities play an important role in establishing the stability conditions for FDEs. In the literature various integral inequalities have been introduced, including the Grönwall inequality, generalised Grönwall inequality, Henry-Grönwall inequality, etc. Below, we state those integral inequalities which are essential for obtaining the results on the Ulam-Hyers stability.
Theorem 2.1 ([34, Grönwall’s inequality]). Suppose that u(t) and v(t) are continuous real-valued functions defined on 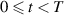 (
(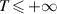 ) with
) with 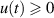 . Assume that u and v satisfy
. Assume that u and v satisfy
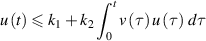
on 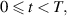 where k1 and k2 are constants with
where k1 and k2 are constants with 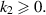 Then,
Then,
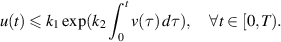
Theorem 2.2 ([83, Henry-Grönwall inequality]). Suppose that 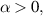
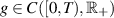 is a non-decreasing function and
is a non-decreasing function and 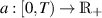 is a locally integrable non-decreasing function; moreover, suppose that u(t) is locally integrable non-negative with
is a locally integrable non-decreasing function; moreover, suppose that u(t) is locally integrable non-negative with
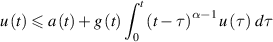
on 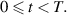 Then,
Then,
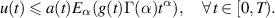
Another important element in the analysis of FDEs are fixed point theorems, without which it is very difficult (actually almost impossible) to study the existence and uniqueness of non-linear FDEs. Fixed point theorems are nowadays the most widely used tool for studying the Ulam-Hyers stability of FDEs. For details on the application of fixed point theorems to Ulam-Hyers stability of functional equations we refer to the survey paper [16] Details on fixed point theorems are described in the monograph [53]. Below, we state those fixed point theorems which are essential for obtaining the results on the Ulam-Hyers stability.
Theorem 2.3 ([53, Banach Fixed Point Theorem]). Let 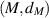 be a complete metric space. Let
be a complete metric space. Let 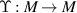 be a contraction map with the Lipschitz constant L < 1. If there exists a non-negative integer k such that
be a contraction map with the Lipschitz constant L < 1. If there exists a non-negative integer k such that 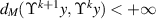 for some
for some 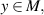 then
then
- (i)the sequence
 converges to a fixed point
converges to a fixed point  of ϒ,
of ϒ, - (ii)
 is the unique fixed point of ϒ in
is the unique fixed point of ϒ in  ,
, - (iii)if
 then
then  .
.
For a given FDE, the Banach fixed point theorem is not only helpful to prove the Ulam-Hyers stability of the problem but it also help to estimate the Ulam-Hyers constant.
Theorem 2.4 ([53, Krasnoselskii’s fixed point theorem]). Let 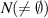 be a closed, convex subset of a Banach space M and
be a closed, convex subset of a Banach space M and 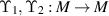 be two operators satisfying
be two operators satisfying
- (i)
 whenever
whenever 
- (ii)
 is continuous and compact,
is continuous and compact, - (iii)
 is a contraction operator.
is a contraction operator.
Then there exists 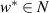 such that
such that 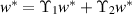 .
.
Theorem 2.5 ([53]). Let X be a Banach space and 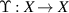 a completely continuous operator. If the set
a completely continuous operator. If the set
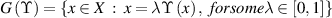
is bounded, then ϒ has a fixed point.
Now, we introduce the concept of the Ulam-Hyers stability for FDEs. Consider the general FDE:
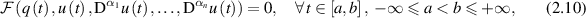
where, ![$u:[a,b]\to X,$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn67.gif) (
(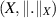 is a norm linear space),
is a norm linear space), 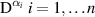 are fractional-order differential operators with
are fractional-order differential operators with 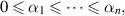 and
and ![$q:[a,b]\to X$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn71.gif) is a given function.
is a given function.
Given 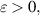 and
and ![$\varphi:[a,b]\to\mathbb{R}_+$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn73.gif) . Suppose
. Suppose ![$v:[a,b]\to X$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn74.gif) satisfy one of the following inequalities:
satisfy one of the following inequalities:
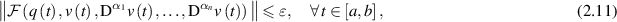
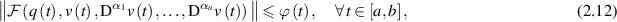
Definition 2.8 (Ulam-Hyers stability). The FDE (2.10) is Ulam-Hyers stable if there exists a positive constant L > 0, such that for each ε > 0 and for each solution v of inequality (2.11) there exists an exact solution u of (2.10) with

Such an L is often called Ulam-Hyers constant, and it is independent of ε.
Definition 2.9 (Ulam-Hyers-Rassias stability). The FDE (2.10) is Ulam-Hyers-Rassias stable, if there exists a positive constant L > 0 such that for each solution v of inequation (2.12) there exists a solution v of (2.10) with4

Hereafter, if the time interval and/or T (defined below) are finite, then the so-called stability is in the sense of finite time.
2.1. Useful tools to analyse the Ulam-Hyers stability
As a summary of this section we list the three main classes of tools to analyse the Ulam-Hyers stability of FDEs.
(i) Fixed point approach: This approach applies to non-linear problems. The most frequently used fixed point theorems to establish the Ulam-Hyers stability for FDEs are the Banach fixed point theorem, the non-linear alternative of the Leray-Schauder type, Krasnoselskii’s and Schauder’s fixed point theorems, etc.
(ii) Integral transforms approach: When a given problem is linear, then integral transform approach will be a good choice to analyse the Ulam-Hyers stability of the problem. The most commonly used integral transforms are the Laplace, Mellin, Sumudu, and Fourier transforms, etc.
(iii) Functional inequalities approach: This plays a vital role for estimating the Ulam-Hyers constant. For some cases this approach helps directly to establish the Ulam-Hyers stability results but in most cases it is used along with the fixed point or integral transform approach. The most frequently used functional inequalities are Grönwall’s inequality, the generalised Grönwall’s inequality, Henry-Grönwall’s inequality, the comparison theorem of differential equations, integral inequalities, etc.
3. Relation between Lyapunov and Ulam-Hyers stability
In general, the Lyapunov and Ulam-Hyers stabilities are independent concepts. For instance, we can have the notion of Ulam-Hyers stability for any functional Equation, but the concept of Lyapunov stability is confined to an equation representing the dynamical system. If we turn to dynamic systems, the Lyapunov stability deals in studying the behaviour of the solutions of a dynamical system near the equilibrium points of the system, whereas the Ulam-Hyers stability mainly applies to finding an exact solution near an approximate solution of the system. In this section, we approach the connection between Lyapunov’s and Ulam-Hyers’ stability concepts in the case of dynamical systems.
Consider the fractional differential equation in the dynamical systems

where 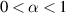 ,
, 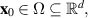 and
and 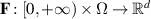 is a continuous function.
is a continuous function.
Definition 3.1. A vector 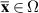 is said to be an equilibrium point of the first differential equation of the system (3.1) if
is said to be an equilibrium point of the first differential equation of the system (3.1) if 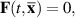 for all
for all 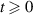 . Define the set
. Define the set 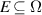 the collection of all such equilibrium points.
the collection of all such equilibrium points.
Denote 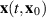 as the solution of the above differential equation (3.1) starting at an initial point
as the solution of the above differential equation (3.1) starting at an initial point 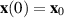 .
.
Definition 3.2 ([37, Lyapunov stability]). [37, Lyapunov stability] The equilibrium point 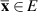 of the system (3.1) is Lyapunov stable, if for every ε > 0 there exists
of the system (3.1) is Lyapunov stable, if for every ε > 0 there exists 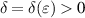 such that
such that
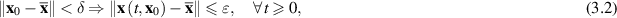
where 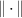 denotes a norm on
denotes a norm on 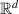 . In other words,
. In other words, 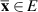 is Lyapunov stable, if given any ε > 0 there exists a neighbourhood
is Lyapunov stable, if given any ε > 0 there exists a neighbourhood 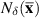 for some δ > 0 such that for each
for some δ > 0 such that for each 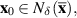 the solution
the solution 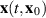 satisfies
satisfies 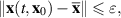 for all
for all 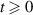 .
.
Definition 3.3 (Ulam-Hyers stability). The differential equation (3.1) is said to be Ulam-Hyers stable if there exists a constant L > 0, such that for every ε > 0 and any function 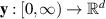 satisfying
satisfying

there exists an exact solution 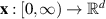 of the differential equation (3.1) such that
of the differential equation (3.1) such that

Remark 3.1. In definition 3.3, the existence of at least one solution 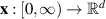 to the differential equation (3.1) that satisfies the inequality (3.4) is sufficient for Ulam-Hyers stability. One obvious such solution can be obtained by choosing an initial value
to the differential equation (3.1) that satisfies the inequality (3.4) is sufficient for Ulam-Hyers stability. One obvious such solution can be obtained by choosing an initial value 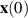 depending on y. In the literature, many authors set
depending on y. In the literature, many authors set 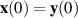 . However, in some cases, there may exist multiple such solutions or even a whole family of solutions in a neighbourhood of
. However, in some cases, there may exist multiple such solutions or even a whole family of solutions in a neighbourhood of 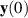 . This fact is demonstrated in the following theorem, established by Onitsuka and Shoji [52] for integer-order differential equations.
. This fact is demonstrated in the following theorem, established by Onitsuka and Shoji [52] for integer-order differential equations.
Theorem 3.1 ([52]). Consider the homogeneous linear differential equation

where I is a nonempty open interval of 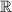 and a is a non-zero real number. Let ε > 0 be a given arbitrary constant. Suppose that a differentiable function
and a is a non-zero real number. Let ε > 0 be a given arbitrary constant. Suppose that a differentiable function 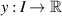 satisfies
satisfies

Then one of the following holds:
- (i)if a > 0 and
 exists, then
exists, then  exists where
exists where  , and any solution x(t) of (3.5) with
, and any solution x(t) of (3.5) with  satisfies that
satisfies that  for all
for all  ;
; - (ii)if a > 0 and
 does not exist, then
does not exist, then  exists, and there exists exactly one solution
exists, and there exists exactly one solution  of (3.5) such that
of (3.5) such that  for all
for all  ;
; - (iii)if a < 0 and
 exists, then
exists, then  exists where
exists where  , and any solution x(t) of (3.5) with
, and any solution x(t) of (3.5) with  satisfies that
satisfies that  for all
for all  ;
; - (iv)if a < 0 and
 does not exist, then
does not exist, then  exists, and there exists exactly one solution
exists, and there exists exactly one solution  of (3.5) such that
of (3.5) such that  for all
for all  .
.
Moreover, they show that for a = 0, the differential equation (3.5) is not Ulam-Hyers stable.
Example 3.1. Consider the simple integer-order differential equation 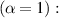

with the initial condition

Let ε > 0 be a given arbitrary number and suppose that the differentiable function 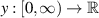 satisfies
satisfies

If a > 0, then by (ii) assertion of theorem 3.1, 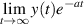 exists. Denote this limit by b. Then, the IVP with initial condition
exists. Denote this limit by b. Then, the IVP with initial condition 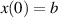 has a unique solution
has a unique solution 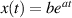 satisfying
satisfying

In other words, the differential equation (3.7) is Ulam-Hyers stable with Ulam-Hyers constant given by 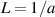 and the solution x(t) which satisfied the inequality (3.10) is unique.
and the solution x(t) which satisfied the inequality (3.10) is unique.
Inequality (3.9) implies

where 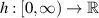 and
and 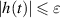 for all
for all 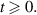 Therefore, from (3.11) and (3.7), we obtain
Therefore, from (3.11) and (3.7), we obtain
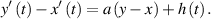
The solution of the above equation is given by
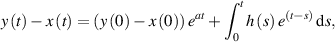
which implies
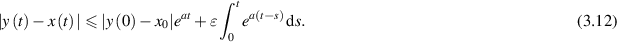
If a < 0, then 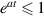 for all
for all 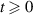 . Choose an initial condition x0 such that
. Choose an initial condition x0 such that

Using these facts in (3.12), we get

where x(t) is the solution of the IVP (3.7) with initial condition 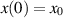 , and x0 satisfying the inequality (3.13). In other words, the differential equation (3.7) is Ulam-Hyers stable with Ulam-Hyers constant
, and x0 satisfying the inequality (3.13). In other words, the differential equation (3.7) is Ulam-Hyers stable with Ulam-Hyers constant 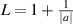 . Moreover, there exists a family of solutions to the IVP (3.7) that satisfy the inequality (3.14), where the initial values x0 belong to an ε-neighbourhood of y(0)
. Moreover, there exists a family of solutions to the IVP (3.7) that satisfy the inequality (3.14), where the initial values x0 belong to an ε-neighbourhood of y(0) 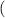 i.e.
i.e. 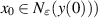 .
.
This example motivates to define a special class of Ulam-Hyers stability, in order to distinguish between two cases:
- (i)The discrete case, where the initial value x0 of the solution
 satisfying inequality (3.4) is distributed discretely
satisfying inequality (3.4) is distributed discretely  as in the case of
as in the case of  .
. - (ii)The continuous case, where the initial value x0 of the solution
 satisfying inequality (3.4) is distributed in some neighbourhood
satisfying inequality (3.4) is distributed in some neighbourhood  of
of 
 as in the case of
as in the case of  .
.
A comparison between Ulam-Hyers and Lyapunov stability makes sense only when the initial condition x0 lies in a neighbourhood of the equilibrium point. Therefore, we introduce the following definition, which we call strong Ulam-Hyers stability.
Definition 3.4 (strong Ulam-Hyers stability). The fractional differential equation (3.1) is said to be strongly Ulam-Hyers stable if there exists a constant L > 0 such that, for every ε > 0 and any vector-valued function 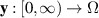 satisfying
satisfying

there exists 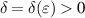 such that
such that
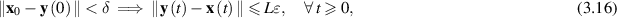
where 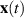 is the solution of the equation (3.1) subject to the initial condition
is the solution of the equation (3.1) subject to the initial condition 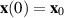 , with x0 satisfying the first inequality in (3.16).
, with x0 satisfying the first inequality in (3.16).
Now, we proceed to introduce a theorem that connects Lyapunov and strong Ulam-Hyers stability for the fractional dynamical system (3.1).
Theorem 3.2. For 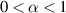 , the strong Ulam-Hyers stability of the fractional differential equation (3.1) implies Lyapunov stability of its equilibrium point.
, the strong Ulam-Hyers stability of the fractional differential equation (3.1) implies Lyapunov stability of its equilibrium point.
Proof. Let ε > 0 be an arbitrary given number. Suppose 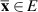 is an equilibrium point of the fractional differential equation (3.1). Then,
is an equilibrium point of the fractional differential equation (3.1). Then,

Given that the fractional differential equation (3.1) is strongly Ulam-Hyers stable, there exists a constant L independent of ε. If we take 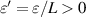 , then we observe that
, then we observe that
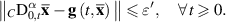
This inequality corresponds to equation (3.15) under the substitution 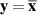 . By Definition 3.4 (Strong Ulam-Hyers stability), there exists
. By Definition 3.4 (Strong Ulam-Hyers stability), there exists 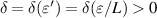 such that
such that
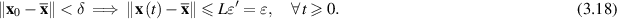
This ends the proof. □
Remark 3.2. The inverse of theorem 3.2 remains an open problem. While Ulam-Hyers stability implies Lyapunov stability in the continuous case, the discrete case− when the existence of a solution 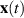 satisfying the Ulam-Hyers inequality (3.4) is determined by a discrete distribution of the initial condition
satisfying the Ulam-Hyers inequality (3.4) is determined by a discrete distribution of the initial condition 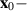 presents advantages over Lyapunov stability. For instance, in the above example for a > 0, the system (3.7) exhibits Ulam-Hyers stability in discrete settings, but the system is not Lyapunov stable for a > 0.
presents advantages over Lyapunov stability. For instance, in the above example for a > 0, the system (3.7) exhibits Ulam-Hyers stability in discrete settings, but the system is not Lyapunov stable for a > 0.
From theorem 3.2 and remark 3.2 above, one can observe that Ulam-Hyers stability is a more general concept in the stability theory of dynamical systems.
4. Ulam-Hyers stability of linear FDEs
In this section, we first consider the simplest form of a linear FDE,
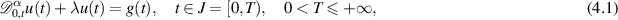
where 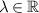 ,
, 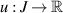 ,
, 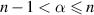 ,
, 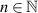 ,
, 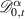 is the Caputo or Riemann–Liouville derivative of order α, and
is the Caputo or Riemann–Liouville derivative of order α, and 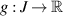 is a given function. The following results addressing the Ulam-Hyers stability was established by Wang and Xu [79, 80] using a Laplace transform.
is a given function. The following results addressing the Ulam-Hyers stability was established by Wang and Xu [79, 80] using a Laplace transform.
Theorem 4.1 ([79]). Given ε > 0, if a function 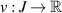 satisfies the inequality
satisfies the inequality

Then, there exists a solution 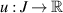 of the FDE (4.1) such that
of the FDE (4.1) such that

Corollary 4.1. If 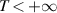 , then the linear FDE (4.1) is Ulam-Hyers stable with an Ulam-Hyers constant
, then the linear FDE (4.1) is Ulam-Hyers stable with an Ulam-Hyers constant 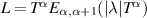 . However, if
. However, if 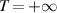 , no conclusion can be drawn from theorem 4.1.
, no conclusion can be drawn from theorem 4.1.
Theorem 4.2 ([80]). Consider the linear FDE (4.1) and let 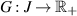 be a given function. Then, if a function
be a given function. Then, if a function 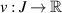 satisfies the inequality
satisfies the inequality

there exists a solution 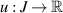 of the linear FDE (4.1) such that
of the linear FDE (4.1) such that
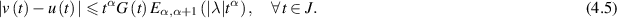
Corollary 4.2. If 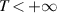 , then the linear FDE (4.1) is Ulam-Hyers-Rassias stable with an Ulam-Hyers-Rassias constant
, then the linear FDE (4.1) is Ulam-Hyers-Rassias stable with an Ulam-Hyers-Rassias constant 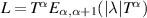 . In contrast, if
. In contrast, if 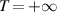 , theorem 4.2 yields no conclusion about its Ulam-Hyers-Rassias stability.
, theorem 4.2 yields no conclusion about its Ulam-Hyers-Rassias stability.
Wang and Li [76] established the Ulam-Hyers stability of the linear FDE for 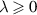 , by using the Laplace transform and evaluated the simplified value of the Ulam-Hyers constant. The result is given in next theorem.
, by using the Laplace transform and evaluated the simplified value of the Ulam-Hyers constant. The result is given in next theorem.
Theorem 4.3 ([76]). Consider the linear FDE (4.1) with 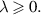 Given ε > 0, if a function
Given ε > 0, if a function 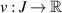 satisfies the inequality
satisfies the inequality

Then, there exists a solution 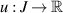 of the FDE (4.1) such that
of the FDE (4.1) such that

Corollary 4.3. If 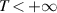 , then the linear FDE (4.1) with
, then the linear FDE (4.1) with 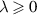 is Ulam-Hyers stable with an Ulam-Hyers constant
is Ulam-Hyers stable with an Ulam-Hyers constant 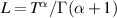 .
.
In the same paper, the authors also analysed the Ulam-Hyers stability of the linear FDE in a Banach space 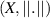 with Caputo derivative of order
with Caputo derivative of order 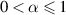 :
:
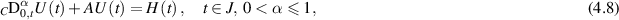
where 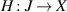 is a continuous function and
is a continuous function and 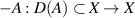 be the generator of a C0-semigroup
be the generator of a C0-semigroup 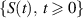 , written as
, written as 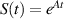 on the Banach space X. Denote
on the Banach space X. Denote 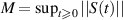 . The result is then
. The result is then
Theorem 4.4 ([76]). Given ε > 0, if a function 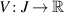 satisfies the inequality
satisfies the inequality

then there exists a solution 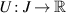 of the FDE (4.8) such that
of the FDE (4.8) such that

Shen and Chen [62] discussed the Ulam stability of the generalised linear FDE with constant coefficients involving a Riemann–Liouville fractional derivative by the Laplace transform method and evaluated the values of the Ulam-Hyers constant in the integral form. First they considered the following linear FDE
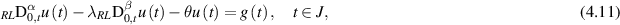
where 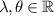 ,
, 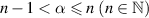 , and
, and 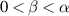 , and established the result.
, and established the result.
Theorem 4.5 ([62]). Let g(t) be a given function such that
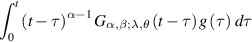
exists for any 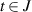 . Suppose that
. Suppose that 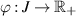 is a function such that the integral
is a function such that the integral
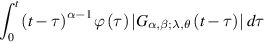
exists for any 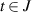 . If a function
. If a function 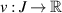 satisfies the inequality
satisfies the inequality
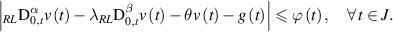
Then, there exists a solution 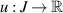 of the linear FDE (4.11) such that
of the linear FDE (4.11) such that
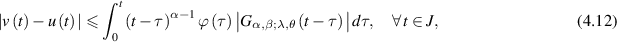
provided that the series
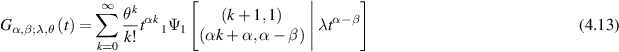
is convergent. Here, 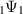 is the hypergeometric function [63].
is the hypergeometric function [63].
For 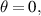 and
and 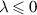 , in the above FDE (4.11), using lemma 2.1 and theorem 4.5, the Ulam-Hyers stability was studied for the linear FDE
, in the above FDE (4.11), using lemma 2.1 and theorem 4.5, the Ulam-Hyers stability was studied for the linear FDE

as a corollary, which is given below.
Corollary 4.4. Let 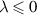 ,
, 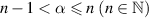 ,
, 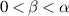 . Given ε > 0, if a function
. Given ε > 0, if a function 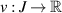 satisfies the inequality
satisfies the inequality
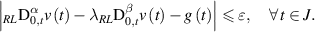
Then there exists a solution 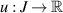 of the linear FDE (4.14) such that
of the linear FDE (4.14) such that
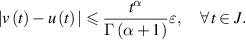
Here, we note that if 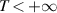 , then the linear FDE (4.14) is Ulam-Hyers stable with an Ulam-Hyers constant
, then the linear FDE (4.14) is Ulam-Hyers stable with an Ulam-Hyers constant 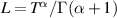 .
.
Finally, they presented the Ulam-Hyers-Rassias stability result for the following generalised linear FDE
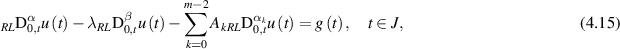
where 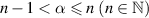 ,
, 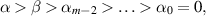
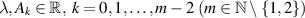 and
and 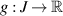 is a given function. The result is
is a given function. The result is
Theorem 4.6 ([62]). Let g(t) be a given function such that
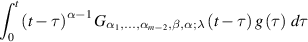
exists for any 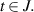 Suppose
Suppose 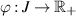 is a function such that the integral
is a function such that the integral
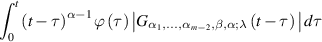
exists for any 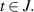 If a function
If a function 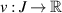 satisfies the inequality
satisfies the inequality
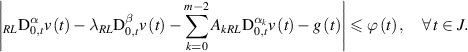
Then, there exists a solution 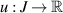 of the generalised linear FDE (4.15) such that
of the generalised linear FDE (4.15) such that
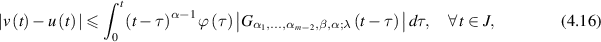
provided that the series
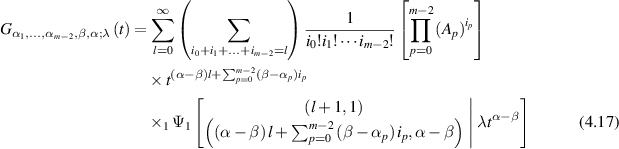
is convergent.
Liu and Li [41] considered the Ulam-Hyers stability of linear FDEs with variable coefficients involving both Riemann–Liouville and Caputo fractional derivatives on a bounded interval ![$I = [0,a]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn218.gif) ,
,

where 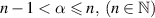 and
and 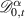 is the Caputo or Riemann–Liouville derivative of order α; moreover,
is the Caputo or Riemann–Liouville derivative of order α; moreover, 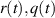 are given continuous functions on
are given continuous functions on ![$I = [0,a]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn222.gif) . By using Grönwall’s inequality, they established the Ulam-Hyers stability result given below.
. By using Grönwall’s inequality, they established the Ulam-Hyers stability result given below.
Theorem 4.7 ([41]). Assume there exists a constant K > 0 such that

for each 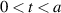 . Given ε > 0, if a function
. Given ε > 0, if a function 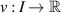 satisfies the inequality
satisfies the inequality
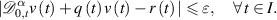
Then, there exists a constant L > 0 and a solution 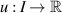 of the FDE (4.18) such that
of the FDE (4.18) such that

where
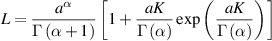
is the Ulam-Hyers constant.
The Ulam-Hyers stability of a general linear functional equation on a Banach space was studied by Takagi et al [66]. They also derived an expression for the best Ulam-Hyers constant. Before we discuss their result, we briefly recall some definitions concerning the Ulam-Hyers stability of linear functional equations.
Let 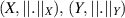 be the normed linear spaces and consider a linear map
be the normed linear spaces and consider a linear map 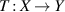 .
.
Definition 4.1 ([66]). We say that the linear map T has Ulam-Hyers stability, if there exists a constant L > 0 with the following property: For any 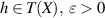 and
and 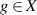 satisfying
satisfying 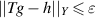 , there exists a
, there exists a 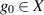 with
with 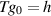 , such that
, such that 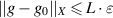 .
.
Now, let T be the bounded linear map and 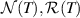 the kernel and range of T respectively. Define an induced one-to-one map
the kernel and range of T respectively. Define an induced one-to-one map 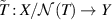 , where
, where 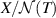 is a quotient space as:
is a quotient space as:
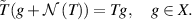
Let 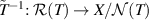 be the inverse of
be the inverse of 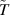 .
.
Theorem 4.8 ([66]). Let 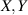 be Banach spaces and
be Banach spaces and 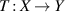 be a bounded linear map. Then, the following statements are equivalent:
be a bounded linear map. Then, the following statements are equivalent:
- (i)T is Ulam-Hyers stable,
- (ii)
 is bounded,
is bounded, - (iii)
 is bounded.
is bounded.
Moreover, if one of the conditions (i), (ii), or (iii) is true. Then, the best Ulam-Hyers constant is given 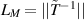 .
.
Based on theorem 4.8, we observe that if a linear functional equation involving bounded linear operators is Ulam-Hyers stable, then the best Ulam-Hyers constant for this equation exists. Thus, by choosing an appropriate functional space and a norm, one can prove the existence of the best Ulam-Hyers constant for the linear FDE.
5. Ulam-Hyers stability of non-linear FDEs
In this section, we present the Ulam-Hyers stability results for non-linear FDEs. Wang et al [78]. addressed the Ulam-Hyers stability of non-linear FDEs involving a Caputo fractional derivative of order 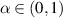 by using the Henry-Grönwall inequality. They also analysed the dependence of data for non-linear FDEs in the case
by using the Henry-Grönwall inequality. They also analysed the dependence of data for non-linear FDEs in the case 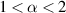 . In essence, they studied the Ulam stability of the following FDE:
. In essence, they studied the Ulam stability of the following FDE:
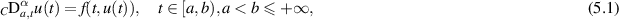
where 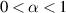 ,
, 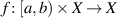 , and
, and 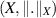 is a Banach space. Under the following assumptions on f:
is a Banach space. Under the following assumptions on f:
(A1) 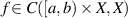 ;
;
(A2) There exists a constant 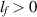 such that
such that
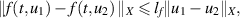
for each 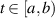 and for all
and for all 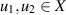 ;
;
(A3) Let 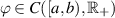 be a non-decreasing function and there exits a constant
be a non-decreasing function and there exits a constant 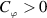 such that
such that
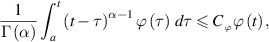
for each 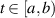 .
.
Theorem 5.1 ([78]). Let assumptions 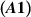 ,
, 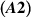 , and
, and 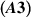 hold. If a function
hold. If a function 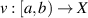 satisfies the inequality
satisfies the inequality
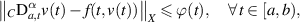
then there exists a solution 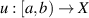 of the FDE (5.1) such that
of the FDE (5.1) such that
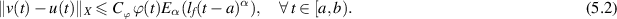
Corollary 5.1. If 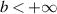 , then the FDE (5.1) is Ulam-Hyers-Rassias stable with
, then the FDE (5.1) is Ulam-Hyers-Rassias stable with 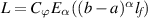 . However, if
. However, if 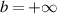 , no conclusion can be drawn from theorem 5.1.
, no conclusion can be drawn from theorem 5.1.
They also established the following Ulam-Hyers stability results for 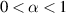 .
.
Theorem 5.2 ([78]). Assume 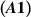 and
and 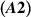 hold. Let ε > 0 be a given number and suppose a function
hold. Let ε > 0 be a given number and suppose a function 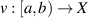 satisfies the inequality
satisfies the inequality
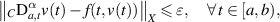
then there exists a solution 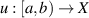 of the FDE (5.1) such that
of the FDE (5.1) such that
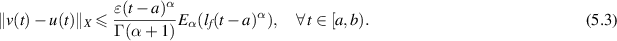
Corollary 5.2. If 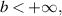 then the FDE (5.1) is Ulam-Hyers stable with
then the FDE (5.1) is Ulam-Hyers stable with
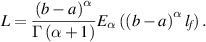
However, if 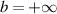 , no conclusion can be drawn from theorem 5.2.
, no conclusion can be drawn from theorem 5.2.
In [77] Wang et al also investigated the Ulam stability of the same non-linear FDE (5.1) with  on a closed and bounded interval by using the Banach fixed point theorem. Further, they improved and simplified the Ulam-Hyers constant. Their results are given below.
on a closed and bounded interval by using the Banach fixed point theorem. Further, they improved and simplified the Ulam-Hyers constant. Their results are given below.
Theorem 5.3 ([77]). For 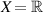 , let assumptions
, let assumptions 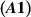 and
and 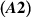 hold over the finite interval
hold over the finite interval ![$[a,b]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn275.gif) . Suppose that
. Suppose that ![$\varphi:[a,b]\to\mathbb{R} _+$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn276.gif) is a continuous function with
is a continuous function with

for each ![$t\in[a,b]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn277.gif) and for some K > 0. Let the constants lf and K satisfy
and for some K > 0. Let the constants lf and K satisfy 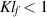 . If a continuously differentiable function
. If a continuously differentiable function ![$v:[a,b]\to \mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn279.gif) satisfies the inequality
satisfies the inequality
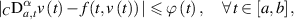
then there exists a unique solution ![$u:[a,b]\to\mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn280.gif) of the FDE (5.1) such that
of the FDE (5.1) such that

In other words, the FDE (5.1) is Ulam-Hyers-Rassias stable.
Here, we notice that the solution u of the FDE (5.1) satisfying (5.5) is unique. In the same paper they also established the Ulam-Hyers stability result given below.
Theorem 5.4 ([77]). For 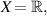 let assumptions
let assumptions 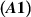 and
and 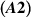 hold on a finite interval
hold on a finite interval ![$[a,a+h]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn284.gif) , h > 0. Let the constant lf satisfy
, h > 0. Let the constant lf satisfy 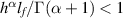 . Given ε > 0, if a continuously differentiable function
. Given ε > 0, if a continuously differentiable function ![$v:[a,a+h]\to\mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn286.gif) satisfies the inequality
satisfies the inequality
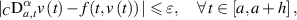
then there exists a unique solution ![$u:[a,a+h]\to\mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn287.gif) of the FDE (5.1) such that
of the FDE (5.1) such that
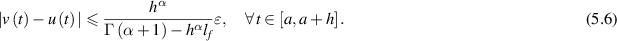
In other words, the FDE (5.1) is Ulam-Hyers stable.
El-Hady and Öğrekci [22] also considered the same non-linear FDE (5.1) with 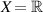 on a closed and bounded interval
on a closed and bounded interval ![$[0, r]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn289.gif) . They removed the assumption (5.4) on the function ϕ and studied the Ulam-Hyers-Rassias stability result by using the Banach fixed point theorem on a generalised metric space. Further, they derived the Ulam-Hyers constant with more flexibility on the parameter than in [77]. The corresponding results are given as follows.
. They removed the assumption (5.4) on the function ϕ and studied the Ulam-Hyers-Rassias stability result by using the Banach fixed point theorem on a generalised metric space. Further, they derived the Ulam-Hyers constant with more flexibility on the parameter than in [77]. The corresponding results are given as follows.
Theorem 5.5 ([22]). For 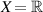 , assume conditions
, assume conditions 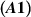 and
and 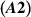 hold on the finite interval
hold on the finite interval ![$[0,r]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn293.gif) , r > 0. Suppose that
, r > 0. Suppose that ![$\varphi:[0,r]\to \mathbb{R}_+$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn294.gif) is a continuous and non-decreasing function; if a continuously differentiable function
is a continuous and non-decreasing function; if a continuously differentiable function ![$v:[0,r]\to\mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn295.gif) satisfies the inequality
satisfies the inequality
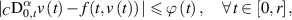
then there exists a unique solution ![$u:[0,r]\to\mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn296.gif) of the FDE (5.1) such that
of the FDE (5.1) such that
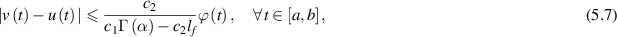
where c1 and c2 are arbitrary positive constants such that the inequalities
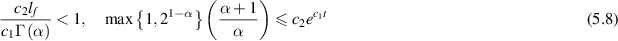
holds for each ![$t\in[0,r.]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn297.gif) In other words, the FDE (5.1) is Ulam-Hyers-Rassias stable.
In other words, the FDE (5.1) is Ulam-Hyers-Rassias stable.
Corollary 5.3. For 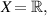 let the assumptions
let the assumptions  and
and 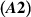 hold on the finite interval
hold on the finite interval ![$[0,r]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn301.gif) , r > 0. Then, the FDE (5.1) is Ulam-Hyers stable with
, r > 0. Then, the FDE (5.1) is Ulam-Hyers stable with ![$L = c_2/[c_1\Gamma(\alpha)-c_2l_f]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn302.gif) , provided that the inequalities (5.8) hold.
, provided that the inequalities (5.8) hold.
Hristove and Abbas [30] investigated the existence of the solution and the Ulam-type stability of an initial value problem (IVP) for non-linear FDEs involving a generalised proportional fractional derivative of Riemann–Liouville fractional type on a closed and bounded interval ![$[a,b]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn303.gif) . They established the results by using the Henry-Gröwall inequality and applied them to a fractional generalisation of a biological population model as an application. They considered the following non-linear FDE (IVP):
. They established the results by using the Henry-Gröwall inequality and applied them to a fractional generalisation of a biological population model as an application. They considered the following non-linear FDE (IVP):
where  ,
,  , and
, and 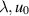 are real constants, and
are real constants, and ![$f:[a,b]\times\mathbb{R}\to\mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn307.gif) is a given continuous function. The solution of the above initial value problem (5.9) exists on a Banach space
is a given continuous function. The solution of the above initial value problem (5.9) exists on a Banach space
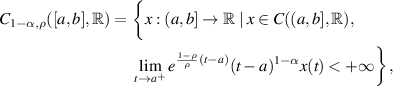
with a norm ![$\|x\|_{C_{1-\alpha,\rho}} = \max_{t\in[a,b]}\left|\exp\left(\frac{ 1-\rho}{\rho}(t-a)\right)(t-a)^{1-\alpha}x(t)\right|$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn308.gif) . The solution
. The solution ![$u\in C_{ 1-\alpha,\rho}([a,b],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn309.gif) satisfies the following integral equation
satisfies the following integral equation
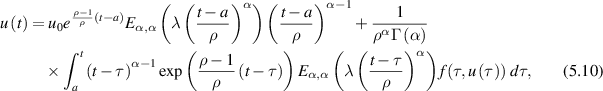
for t > a.
Theorem 5.6 ([30]). Let 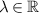 and assume the conditions
and assume the conditions 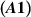 and
and 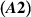 hold with
hold with 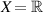 . Let ε > 0 be an arbitrary given number and suppose a function
. Let ε > 0 be an arbitrary given number and suppose a function ![$v\in C_{1-\alpha,\rho}([a,b])$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn314.gif) satisfies the inequality
satisfies the inequality
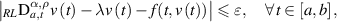
then there exists a solution ![$u\in C_{1-\alpha,\rho}([a,b])$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn315.gif) of the IVP (5.9) such that
of the IVP (5.9) such that

where
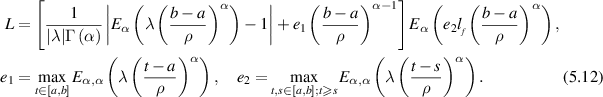
In other words, the FDE (5.9) is Ulam-Hyers stable.
For λ < 0, they proved the Ulam-Hyers-Rassias stability for the FDE (5.9) and estimated the simplified value of the Ulam-Hyers constant as follows.
Theorem 5.7 ([30]). Let λ < 0 and assume the assumptions 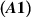 ,
, 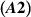 , and
, and 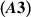 hold on bounded interval
hold on bounded interval ![$[a,b]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn319.gif) with
with 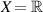 . If a function
. If a function ![$v\in C_{1-\alpha,\rho}([a,b])$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn321.gif) satisfies the inequality
satisfies the inequality
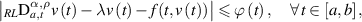
then there exists a solution ![$u\in C_{1-\alpha,\rho}([a,b])$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn322.gif) of the IVP (5.9) such that
of the IVP (5.9) such that

where
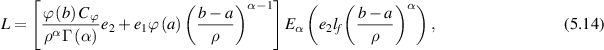
and 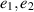 are defined in theorem 5.6.
are defined in theorem 5.6.
In [18] Cuong presented the Ulam-Hyers stability analysis of multi-order FDEs involving the Riemann–Liouville derivative. They established the Ulam stability with respect to a 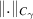 -norm on a
-norm on a ![$C_{\gamma} ([0,T],\mathbb{R}^d)$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn325.gif) space
space 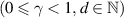 followed by a Bielecki type norm. The
followed by a Bielecki type norm. The ![$C_{\gamma}([0,T],\mathbb{R}^d)$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn327.gif) space is defined as
space is defined as
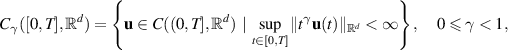
with a norm

where 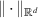 is a norm on
is a norm on 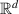 . Basically, they studied the Ulam-type stability for the following initial value FDE (IVP):
. Basically, they studied the Ulam-type stability for the following initial value FDE (IVP):

with initial condition
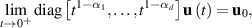
where 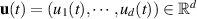 ,
, 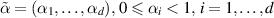 , and
, and ![$\mathbf{f}:[0,T]\times\mathbb{R}^d\to\mathbb{R}^d$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn332.gif) . The Riemann–Liouville multi-order fractional derivative
. The Riemann–Liouville multi-order fractional derivative 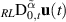 is defined by
is defined by 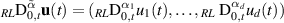 .
.
Lemma 5.1 ([18]). Assume that f is continuous on ![$[0,T]\times\mathbb{R} ^d.$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn335.gif) Then, a function
Then, a function ![$\mathbf{u}\in C((0,T],\mathbb{R}^d)$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn336.gif) is a solution of the IVP (5.16) if and only if it is a solution of the Volterra integral Equation
is a solution of the IVP (5.16) if and only if it is a solution of the Volterra integral Equation
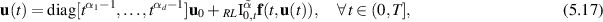
where 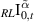 is a multi-order fractional integral operator.
is a multi-order fractional integral operator.
Since the integral equation (5.17) is an equivalent form of the FDE (5.16). Cuong studied the Ulam-Hyers stability of the equivalent integral equation (5.17) instead of the considered FDE (5.16). The result is given below.
Theorem 5.8 ([18]). Assume f is continuous and Lipschitz continuous with respect to the second variable with a Lipschitz constant 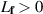 . Let ε > 0 be an arbitrary given number and suppose a function
. Let ε > 0 be an arbitrary given number and suppose a function ![$\mathbf{v}\in C_{1-\alpha_{0}}([0,T],\mathbb{R}^d)$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn339.gif) satisfies the inequality
satisfies the inequality
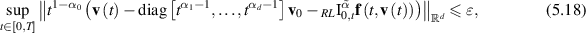
then there exists a solution ![$\mathbf{u}\in C_{1-\alpha_0}([0,T],\mathbb{R}^d)$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn340.gif) of the FDE (5.16) such that
of the FDE (5.16) such that

where 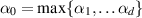 and θ > 0 is chosen large enough such that
and θ > 0 is chosen large enough such that
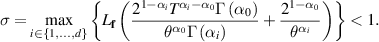
In the other words, the multi-order FDE (5.16) is Ulam-Hyers stable with respect to the 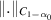 norm.
norm.
6. Fractional-order delay differential equations
A delay differential equation (DDE) is a general class of differential Equation in dynamical systems, occurring naturally when modelling real-world problems. For instance, any feedback control system inherently includes time delays, as sensing information and responding to it takes finite time. Integer-order DDEs have a well-developed theory regarding the existence and stability of solutions [23, 39, 45, 50, 59]. In recent decades, fractional delay differential equations (FDDEs) have received considerable attention due to their applications in dynamical systems and control. For results on the existence and stability of solutions to FDDEs, see [17, 69].
Refaai et al [57] studied the Ulam-type stability of FDDEs involving a Riemann–Liouville fractional derivative in a closed and bounded interval by using the Banach fix point theorem followed by Henry-Gröwall inequality. However, according to our analysis their assumptions and derivations are not correct. For a detailed proof see [57]. Develi and Duman [20] studied the existence of solutions and the Ulam-Hyers stability of FDDEs involving a Caputo fractional derivative by using the Banach fixed point theorem on a Banach space ![$C([-\theta,b],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn343.gif) endowed with the following Bielecki norm.
endowed with the following Bielecki norm.

Concretely, they consider the following delay system:
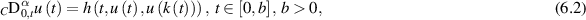

where 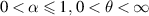 ,
, ![$h\in C([0,b]\times\mathbb{R}^2, \mathbb{R}),\;\zeta\in C([-\theta,0],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn345.gif) , and
, and ![$k\in C([0,b], [-\theta,b])$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn346.gif) with
with 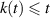 . Under the following assumptions:
. Under the following assumptions:
(A4) ![$h\in C([0,b]\times\mathbb{R}^2,\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn348.gif) ,
, ![$k\in C([0,b], [-\theta,b])$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn349.gif) with
with 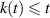 on
on ![$[0,b]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn351.gif) .
.
(A5) There exists a constant ω > 0 such that
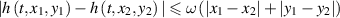
for all 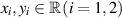 and
and ![$t\in [0,b]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn353.gif) , the following result was established.
, the following result was established.
Theorem 6.1 ([20]). Suppose the assumptions 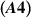 and
and 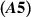 hold. Let ε > 0 be an arbitrary given number and suppose a function
hold. Let ε > 0 be an arbitrary given number and suppose a function ![$v\in C([-\theta,b],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn356.gif) satisfies the inequality
satisfies the inequality
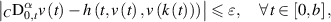
then there exists a solution ![$u\in C([- \theta,b],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn357.gif) of the delay system (6.2) such that
of the delay system (6.2) such that
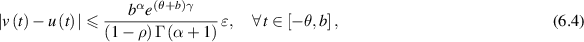
where γ > 0 is an appropriate real number such that 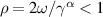 .
.
Recently, Benzarouala and Tunc [10] studied the Ulam-type stability of the FDDEs involving a Caputo derivative with n-multiple variable time delays:
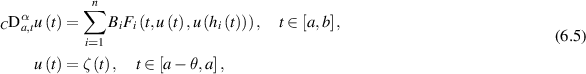
where ![$0 \lt \alpha\unicode{x2A7D}1,\;\zeta\in C([a- \theta,a],\mathbb{R}),\;F_i\in C([a,b] \times\mathbb{R}\times\mathbb{R},\mathbb{R}),\; B_i\in\mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn359.gif) for
for 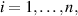 and
and ![$h_i\in C([a,b],[a-\theta,b])$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn361.gif) with
with 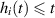 such that
such that 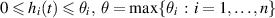 .
.
The result was established by the utilisation of the Banach fixed point theorem on a complete metric space X given by
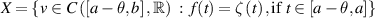
endowed with the metric
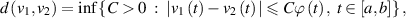
where ![$\varphi:[a,b]\to\mathbb{R}_+$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn364.gif) is a continuous function. Along with the following assumptions:
is a continuous function. Along with the following assumptions:
(A6) For every ![$i = 1,\cdots,n,\;F_i\in C([a,b]\times\mathbb{R} \times\mathbb{R},\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn365.gif) there exists positive constants ωi and
there exists positive constants ωi and 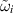 such that
such that
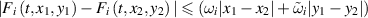
for every ![$t\in [a,b]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn367.gif) and for all
and for all 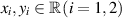 .
.
(A7) Let ![$\varphi\in C([a-\theta,b],\mathbb{R}_+)$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn369.gif) be a non-decreasing function and there exits a constant
be a non-decreasing function and there exits a constant 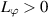 such that
such that
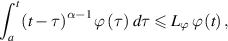
for each ![$t\in[a,b]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn371.gif) .
.
Theorem 6.2 ([10]). Assume that the assumptions 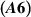 and
and 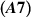 hold. If a function
hold. If a function ![$v\in C^1([a-\theta,b],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn374.gif) satisfies the inequalities
satisfies the inequalities
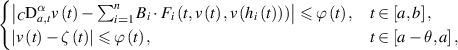
then there exists a unique solution ![$u\in C([a-\theta,b],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn375.gif) of the FDDE (6.5) such that
of the FDDE (6.5) such that
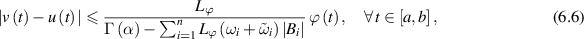
provided that 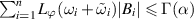 . In other words, the FDDE (6.5) is Ulam-Hyers-Rassias stable.
. In other words, the FDDE (6.5) is Ulam-Hyers-Rassias stable.
As a corollary of theorem 6.2, the following Ulam-Hyers stability results were also established.
Corollary 6.1. Assume the conditions of theorem 6.2 hold, along with assumption 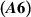 . Let ε > 0 be an arbitrary given number and suppose a function
. Let ε > 0 be an arbitrary given number and suppose a function ![$v\in C^1([a-\theta,b],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn378.gif) satisfies the inequalities
satisfies the inequalities
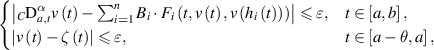
then there exists a unique solution ![$u\in C([a-\theta,b],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn379.gif) of the FDDE (6.5) such that
of the FDDE (6.5) such that
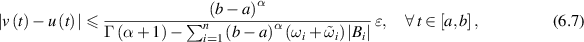
provided that 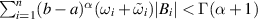 . In other words, the FDDE (6.5) is Ulam-Hyers stable.
. In other words, the FDDE (6.5) is Ulam-Hyers stable.
7. Fractional-order boundary value problem
In the previous section, we discussed the work carried out on the Ulam-type stability of the different classes of FDEs subject to given initial conditions. In this section, some basic Ulam-type stability results of fractional-order boundary value problems (BVPs) will be presented. Applying the fractional-oder model to real-world problems needs a physically interpretable initial/boundary condition which contains 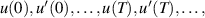 etc. There have been multiple studies of the Ulam-type stability of fractional-order BVPs [2, 5, 11, 27, 64, 73]. Here we present a few of these results on the Ulam-type stability of the fractional-order BVP involving Caputo fractional derivatives. For the existence of solutions of the different classes of a fractional BVP with a Caputo fractional derivative of order
etc. There have been multiple studies of the Ulam-type stability of fractional-order BVPs [2, 5, 11, 27, 64, 73]. Here we present a few of these results on the Ulam-type stability of the fractional-order BVP involving Caputo fractional derivatives. For the existence of solutions of the different classes of a fractional BVP with a Caputo fractional derivative of order 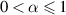 and
and 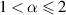 see the survey paper by Agarwal et al [1] and the book by Ali et al [5]. As in the case of an integer-order BVP, the solution of the fractional-order BVP is expressed with the help of the Green’s function.
see the survey paper by Agarwal et al [1] and the book by Ali et al [5]. As in the case of an integer-order BVP, the solution of the fractional-order BVP is expressed with the help of the Green’s function.
Ali et al [5]. analysed the Ulam-type stability of the following fractional-order BVP:
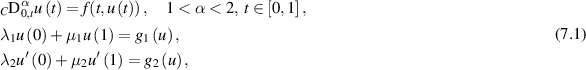
where ![$g_i\;(i = 1,2):C([0,1],\mathbb{R})\to\mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn384.gif) are non-local continuous functions,
are non-local continuous functions, ![$f:C([0,1]\times\mathbb{R},\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn385.gif) , and
, and 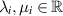 with
with 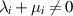 for
for 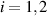 . The result is obtained by using the Banach fixed point theorem. The solution of the BVP (7.1) is given by
. The result is obtained by using the Banach fixed point theorem. The solution of the BVP (7.1) is given by

where
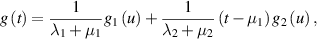
and 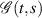 is the Green’s function of the BVP (7.1) given by
is the Green’s function of the BVP (7.1) given by
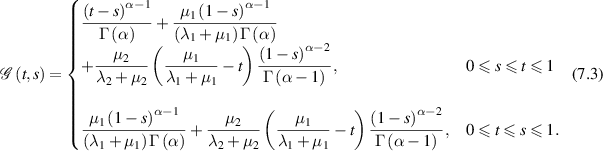
To established the result, they assumed the following property of g:
(A8) For ![$u_1,u_2\in C([0,1],\mathbb{R}),$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn390.gif) there exists
there exists 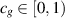 , such that
, such that

where ![$\|u\|_{\infty} = \sup_{t\in[0,1]}\Big\{|u(t)|\;:\; u\in C([0,1],\mathbb{R})\Big\}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn392.gif) .
.
Theorem 7.1 ([5]). Assume the assumption 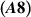 holds and let
holds and let ![$f\in C([0,1] \times\mathbb{R},\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn394.gif) be Lipschitz-continuous with respect to the second variable with a Lipschitz constant Lf. Let
be Lipschitz-continuous with respect to the second variable with a Lipschitz constant Lf. Let ![$\varphi\in C([0,1], \mathbb{R}_+)$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn395.gif) be a non-decreasing function and there exists a constant
be a non-decreasing function and there exists a constant 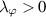 such that
such that 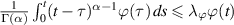 for each
for each ![$t\in[0, 1]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn398.gif) . If a function
. If a function ![$v\in C([0,1], \mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn399.gif) satisfies the inequality
satisfies the inequality
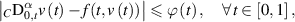
then there exists a unique solution ![$u\in C([0,1],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn400.gif) of the fractional-order BVP (7.1) such that
of the fractional-order BVP (7.1) such that
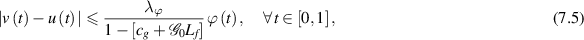
provided that 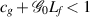 , where
, where ![$\mathscr{G}_{0} = \max_{t\in [0,1]}\int_0^1|\mathscr{G}(t,s)|\,ds$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn402.gif) . In other words, the fractional-order BVP (7.1) is Ulam-Hyers-Rassias stable.
. In other words, the fractional-order BVP (7.1) is Ulam-Hyers-Rassias stable.
Next, they also established the Ulam-Hyers stability result:
Theorem 7.2 ([5]). Given the assumption 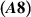 and
and ![$f\in C([0,1]\times\mathbb{R}, \mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn404.gif) be Lipschitz-continuous with respect to the second variable with a Lipschitz constant Lf. Let ε > 0 be an arbitrary given number and suppose a function
be Lipschitz-continuous with respect to the second variable with a Lipschitz constant Lf. Let ε > 0 be an arbitrary given number and suppose a function ![$v\in C([0,1],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn405.gif) satisfies the inequality
satisfies the inequality
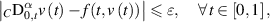
then there exists a unique solution ![$u\in C([0,1],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn406.gif) of the fractional-order BVP (7.1) such that
of the fractional-order BVP (7.1) such that
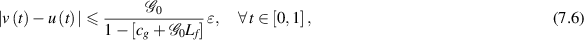
provided that 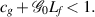 In other words, the fractional-order BVP (7.1) is Ulam-Hyers stable.
In other words, the fractional-order BVP (7.1) is Ulam-Hyers stable.
Chen et al [14] investigated the Ulam-Hyers stability of a class of multi-term non-linear fractional-order BVPs involving a Caputo fractional derivative:
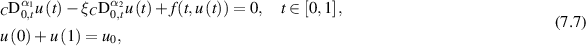
where 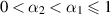 ,
, ![$f\in C([0,1]\times\mathbb{R},\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn409.gif) , and
, and 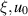 are given constants such that
are given constants such that 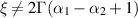 . The solution of the fractional BVP (7.7) is given by
. The solution of the fractional BVP (7.7) is given by
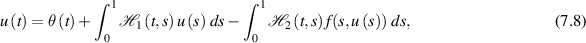
where
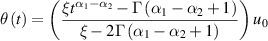
as well as
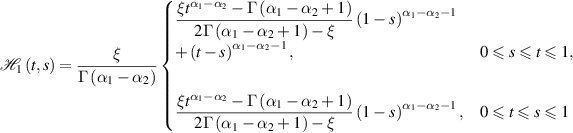
and
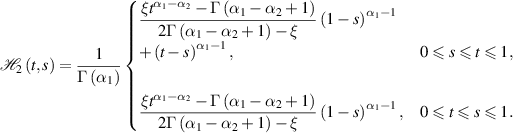
By using the Banach fixed point theorem and the Grönwall inequality, they obtained the following result.
Theorem 7.3 ([14]). Assume ![$\mathscr{M}_{0} = \displaystyle\max_{t\in [0,1]} \int_{0}^{1}|\mathscr{H}_{1}(t,s)|\, ds \lt 1$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn412.gif) and
and 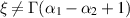 . Let
. Let ![$f\in C([0,1]\times\mathbb{R},\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn414.gif) be Lipschitz continuous with respect to second variable with a Lipschitz constant Lf. Given any
be Lipschitz continuous with respect to second variable with a Lipschitz constant Lf. Given any 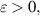 if a function
if a function ![$v\in C([0,1],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn416.gif) satisfies the inequality
satisfies the inequality
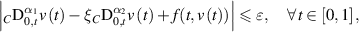
then there exists a unique solution ![$u\in C([0,1],\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn417.gif) such that
such that
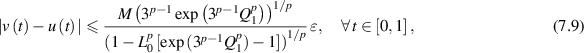
where
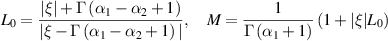
and
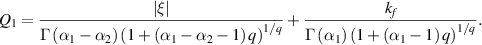
Moreover, 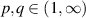 such that
such that 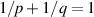 and
and 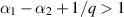 .
.
From the above results, we note that compared to the fractional-order initial value problem (IVP) the Ulam-type stability for the fractional-order BVP is quite complex to analyse. One of the reasons is that the IVP utilises different methods such as integral transform method, fixed point method and different integral inequalities. Another reason may be that the solution of the IVP can be written in the form a simple Volterra integral Equation, whereas the solution of the BVP appears as a mixed (Volterra and Fredholm) integral equation.
8. Fractional-order impulsive differential equations
An impulsive differential equation is a special class of differential Equation used to describe real-world phenomena more accurately, including evolutionary processes characterised by abrupt changes of the state at certain instants. In the literature two familiar impulses are found: instantaneous impulses and non-instantaneous impulses. In the case of instantaneous impulses, the time interval of the changes is relatively short in comparison to the total duration of the process, while in the non-instantaneous case, an impulsive action starts at an arbitrary point in time and remains active for a finite time interval. For details on the theory of the impulsive differential equation see the monographs by Lakshmikantham et al [38], Bainov [8] and Wang et al [74]. In 2013, Hernández [28] and O’Regan introduced a new class of impulsive differential Equation with non-instantaneous impulses and studied the existence of a mild solution. Agarwal et al [3] analysed a Caputo FDE with non-instantaneous impulses. For a detailed survey on non-instantaneous impulses on integer- and FDEs, we refer to the monograph by Agarwal et al [4].
Wang et al [81] studied the existence of the solution and the Ulam-Hyers stability of non-linear impulsive FDEs with Caputo derivative on the finite interval ![$J = [0,T]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn421.gif) :
:
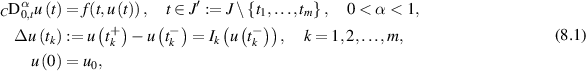
where 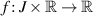 is jointly continuous,
is jointly continuous, 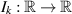 and
and 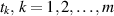 , satisfy
, satisfy 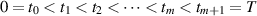 ,
, 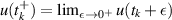 and
and 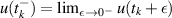 represent the right and left limits of u(t) at
represent the right and left limits of u(t) at 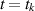 . They established the results by using the fixed point theorem on a Banach space
. They established the results by using the fixed point theorem on a Banach space ![$PC(J,\mathbb{R}) = \big\{u:J\to\mathbb{R}:u\in C\left((t_k,t_{k +1}],\mathbb{R}\right),k = 0,1,\ldots,m;\;u(t^+_k),u(t^-_k)$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn429.gif) exist with
exist with 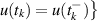 endowed with the norm
endowed with the norm
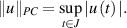
Lemma 8.1 ([81]). Let 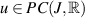 satisfy the following inequality
satisfy the following inequality
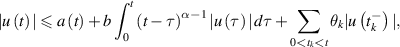
where a(t) is non-negative continuous and non-decreasing function on J and 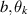 are non-negative constants. Then,
are non-negative constants. Then,
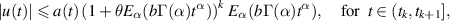
where 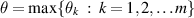 .
.
Definition 8.1 ([81]). A function 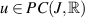 is a solution of the impulsive FDE (8.1) if u satisfies
is a solution of the impulsive FDE (8.1) if u satisfies
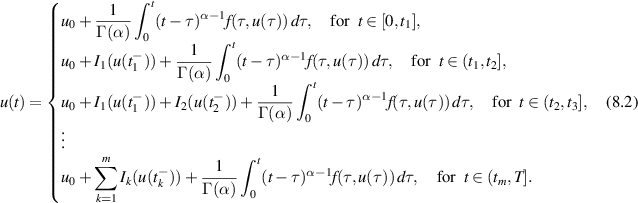
They assume the following assumptions to establish the main results:
(A9) For arbitrary 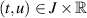 , there exist
, there exist 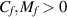 and
and 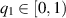 such that
such that 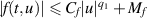 .
.
(A10) For arbitrary 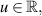 there exist
there exist 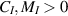 and
and 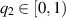 such that
such that 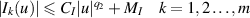 .
.
(A11) There exists a constant 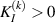 such that
such that 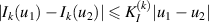 , for all
, for all 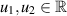 and
and 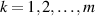 .
.
Theorem 8.1. Let the assumptions 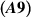 ,
, 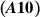 ,
, 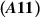 hold and
hold and 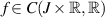 be a Lipschitz-continuous function with respect to the second variable with a Lipschitz constant Lf. Let
be a Lipschitz-continuous function with respect to the second variable with a Lipschitz constant Lf. Let 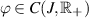 be a non-decreasing function and there exists a constant
be a non-decreasing function and there exists a constant 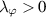 such that
such that 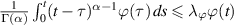 for each
for each 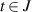 . If a function
. If a function 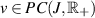 satisfies the inequalities
satisfies the inequalities
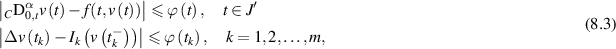
then there exists a unique solution 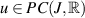 of the impulsive FDE (8.1) such that
of the impulsive FDE (8.1) such that

where 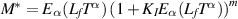 and
and 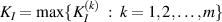 . In other words, the impulsive FDE BVP (8.1) is Ulam-Hyers-Rassias stable.
. In other words, the impulsive FDE BVP (8.1) is Ulam-Hyers-Rassias stable.
Ding [21] studied the Ulam-Hyers stability of delay FDEs with instantaneous impulses by using the Banach fixed point theorem and the abstract Grönwall inequality.
Wang et al [82] investigated the existence of the solution and Ulam-type stability of non-linear FDEs with non-instantaneous impulses with a Caputo derivative on the finite interval ![$J = [0,T]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn459.gif) :
:
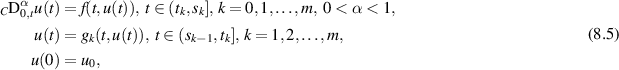
where 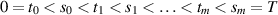 ,
, 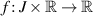 is continuous, and
is continuous, and ![$g_k:[s_{k-1},t_k]\times\mathbb{R}\to\mathbb{R}$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn462.gif) is continuous for each
is continuous for each 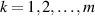 , the so-called non-instantaneous impulses.
, the so-called non-instantaneous impulses.
Definition 8.2 ([82]). A function 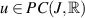 is a mild solution of the FDE (8.5) if u satisfies
is a mild solution of the FDE (8.5) if u satisfies
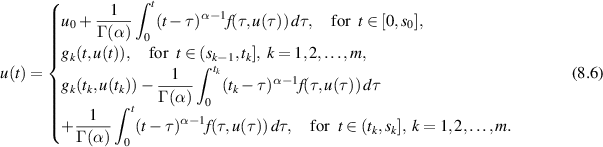
They introduced the concepts of generalised Ulam-Hyers stability for the non-instantaneous impulsive FDE (8.5).
Let ε > 0 and  be non-decreasing. Consider the following inequalities:
be non-decreasing. Consider the following inequalities:
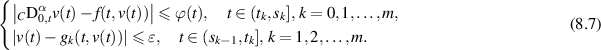
Definition 8.3 ([82]). The non-instantaneous impulsive FDE (8.5) is said to be generalised Ulam-Hyers stable with respect to 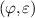 if there exists a constant L > 0 such that, for each solution
if there exists a constant L > 0 such that, for each solution 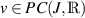 of the inequality (8.7) there exists a solution
of the inequality (8.7) there exists a solution 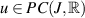 of the FDE (8.5) with
of the FDE (8.5) with
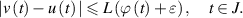
They assume the following assumptions to establish the main results:
(A12) ![$g_k\in C([s_{k-1},t_k]\times\mathbb{R},\mathbb{R})$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn469.gif) and there are positive constants
and there are positive constants 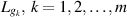 such that
such that 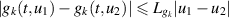 , for each
, for each ![$t\in(s_{k-1},t_k]$](https://content.cld.iop.org/journals/1751-8121/58/45/453001/revision2/aae189eieqn472.gif) , and for all
, and for all 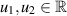 .
.
(A13) The function 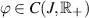 is a non-decreasing function. There exist
is a non-decreasing function. There exist 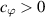 and
and 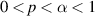 such that
such that
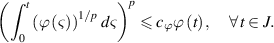
Theorem 8.2 ([82]). Assume 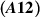 and
and 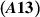 hold, and let
hold, and let 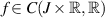 be Lipschitz-continuous with respect to the second variable with a Lipschitz constant Lf. If a function
be Lipschitz-continuous with respect to the second variable with a Lipschitz constant Lf. If a function 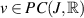 satisfies the inequality (8.7). Then, there exists a unique solution
satisfies the inequality (8.7). Then, there exists a unique solution 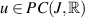 of the FDE (8.5) as given in equation (8.6) such that
of the FDE (8.5) as given in equation (8.6) such that
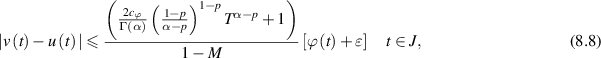
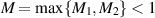 , and where
, and where 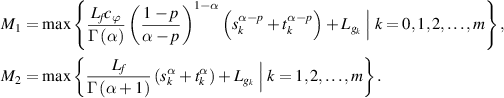
Similarly, Shankar and Bora [60, 61] established the Ulam-Hyers and generalised Ulam-Hyers stability of the non-instantaneous impulsive integro-differential equation involving a Caputo derivative by using the Banach fixed point theorem and applied the obtained results to fractional RLC circuits as an application.
9. Conclusions
We presented a brief survey and introduced the methods to deal with the Ulam-Hyers stability of FDEs. The survey covers recent contributions in this area for various classes of FDEs such as linear FDEs, non-linear FDEs, delay FDEs, fractional-order BVP, and impulsive FDEs. We also established a connection between the Lyapunov and Ulam-Hyers stability for dynamical systems and pointed out that the Ulam-Hyers stability is more general than the Lyapunov stability.
From this survey, one can observe that most of the results on Ulam-Hyers stability for FDEs have been established on a bounded interval, and none of the authors have tried to estimate the best Ulam-Hyers constant even for linear FDEs. As this field has large relevance in practical applications of FDEs, both more work on the development of the theoretical framework and establishing solutions for concrete problems are needed.
Acknowledgments
RM acknowledges funding from the German Research Foundation (DFG, Grants ME 1535/12-1 and ME 1535/22-1). CL acknowledges funding from the National Natural Science Foundation of China (Grants 12271339 and 12572013).
Data availability statement
No new data were created or analysed in this study.
Footnotes
- 4
An inequation denotes a mathematical relation that is either an inequality or a “not equal to” relation between two values.